I What are the values of ##x## for which the series (ln n)^x converges?

[Happiness]

Find the values of $x$ for which the following series is convergent.

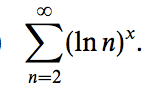
I compared the series with the harmonic series and deduced it is always divergent. I used $y^p<e^y$ for large $y$. I used a different method from the answer given, which I don't understand.

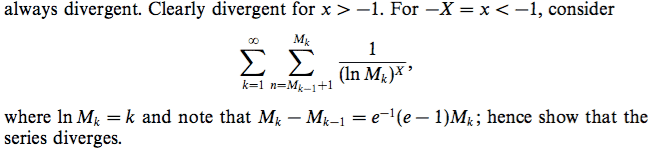
When $k=1$, $M_1=e=2.72$ and $M_0=1$. Since $M_0+1\leq n\leq M_1$, we have $n=2$, giving us the term $\frac{1}{1^X}$.

When $k=2$, $M_2=e^2=7.39$ and $M_1=e=2.72$. Since $M_1+1\leq n\leq M_2$, we have $n=4, 5, 6, 7$, giving us the terms $\frac{1}{2^X}+\frac{1}{2^X}+\frac{1}{2^X}+\frac{1}{2^X}$.

Finding the possible values of $n$ is troublesome.

Is there a typo in the given answer?

 

[mfb]

You get of the order of e terms of 1/1^X, e² terms of 1/2^X, e³ terms of 1/3^X and so on (up to the constant prefactor). Following the same logic as your approximation, $\displaystyle \frac{e^n}{n^X}$ grows to infinity instead of going to zero.

 

[Happiness]

You get of the order of e terms of 1/1^X, e² terms of 1/2^X, e³ terms of 1/3^X and so on (up to the constant prefactor). Following the same logic as your approximation, $\displaystyle \frac{e^n}{n^X}$ grows to infinity instead of going to zero.

Why is the series in the question and the series in the answer equivalent?

Their first terms are clearly different. The former's is $\frac{1}{(\ln 2)^X}$ while the latter's is $\frac{1}{1^X}$.

If they are not equivalent, how do we show that the former is always bigger than the latter for every term?

 

[mfb]

The first fraction is always larger than the second by construction of the M_k. So your series is larger than a divergent series.

 

[Happiness]

The first fraction is always larger than the second by construction of the M_k. So your series is larger than a divergent series.

Could you explain how? I don't see it.

 

[mfb]

ln(2) < 1
ln(3) < 2, ln(4) < 2, ln(5) < 2, ln(6) < 2, ln(7) < 2

Therefore 1/ln(2)^X > 1/1^X and so on for positive X.

 

[Happiness]

The given answer is so complicated vs if we just compare the series with the harmonic series.

 

[mfb]

The given answer is so complicated vs if we just compare the series with the harmonic series.

How do you do that for x=-3?

 

[Happiness]

How do you do that for x=-3?

Let $y=\ln n$. For large $n, y^3<e^y$. So $(\ln n)^3<n$. Then $\frac{1}{(\ln n)^3}>\frac{1}{n}$. The series is bigger than the harmonic series for every term. Hence it is also divergent.

 

[mfb]

Ah right, that works as well, and it is easier.