What are the voltages generated from this current source?

[zenterix]

Homework Statement

The circuit shown below contains two nonlinear devices and a current source. The characteristics of the two devices are given. Determine the voltage $v$ for

Relevant Equations

(a) $i_S=1$A, (b) $i_S=10$A, (c) $i_S=1\cos{t}$.

Here is the circuit and the v-i characteristics

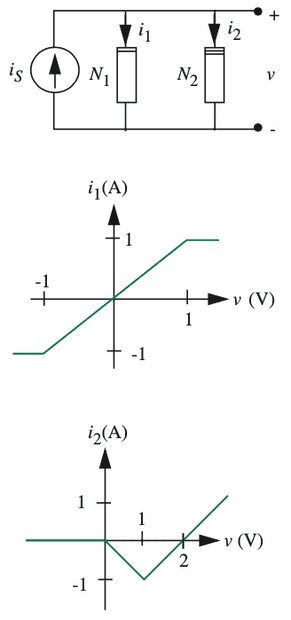
KCL gives us $i_S=i_1+i_2$.

Thus, (a) and (b) are solved quickly by noting that for $v\in [0,1]$ we have $i_1+i_2=0$ so $v$ can't be in this interval for a positive current.

If we try $v\in [1,\infty)$ then we get $i_S=1+(-2+v)=v-1$.

Thus, $i_S=1$A gives $v=2$V and $i_S=10$A gives $v=11$V.

My question is about item (c) where $i_S=\cos{(t)}$.

What I did was consider four different cases related to the possible value of $v$. All I did in each case was consider the KCL equation in the context of a restriction on values of $v$. Note that only cases 2 and 3 are relevant to the solution of (c).

Case 1: $v\in [1,\infty)$

From the KCL equation, $i_S=-1+v$, which graphically is

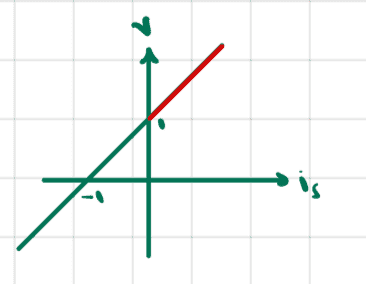
and we see that $v$ satisfies our constraint when $i_S\geq 1$.

Case 2: $v\in [0,1)$

Here we have simply $i_S=0$.

Case 3: $v\in [-1,0)$

Then, $i_S=v$

Case 4: $v \in (-\infty, -1)$

Then, $i_S=-1$

Putting all of this together we have

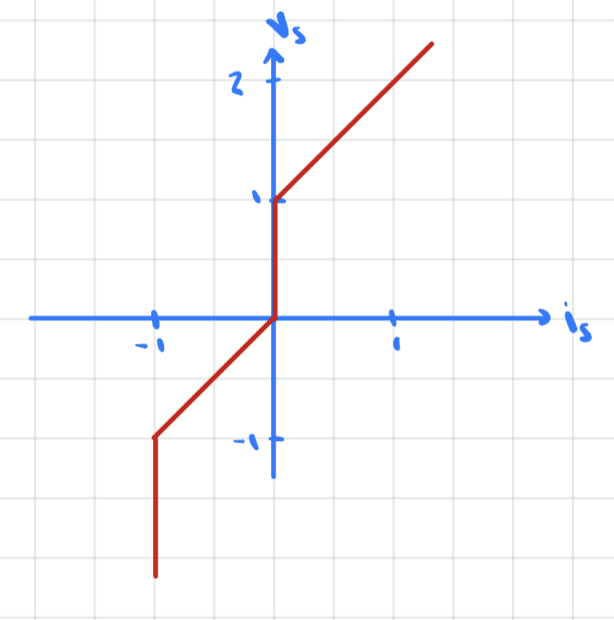
We know that $i_S$ is a sinusoid that varies between -1 and 1. Thus, $v$ takes on values between -1 and 2.

It seems that

$$v(i_S)=\begin{cases} i_S+1,\ \ \ \ \ i_S\in (0,1) \\ i_S,\ \ \ \ \ i_S\in [-1,0] \end{cases}$$

$$v(t)=\begin{cases} \cos{(t)}+1,\ \ \ \ \ t\in (-\pi/2,\pi/2) \\ \cos{(t)},\ \ \ \ \ t\in (\pi/2,3\pi/2) \end{cases}$$

My question is what happens when $i_S=0$?

 

[zenterix]

@berkeman What difference does it make if I write v-i characteristics rather than V-I characteristics that you edited my title?

Agarwal, "Foundations of Analog and Digital Circuits":

 

[berkeman]

@berkeman What difference does it make if I write v-i characteristics rather than V-I characteristics that you edited my title?

Good question. For stand-alone symbols, it's more common in my experience to use V and I. However if you are writing the time functions explicitly, then $v(t)$ $i(t)$ would probably be more appropriate. Remember that lowercase "i" or "j" is often used for complex exponents.