What Charge Does the Third Sphere Acquire?

[utkarshakash]

Homework Statement

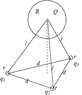
Three identical metal spheres are uncharged at the vertices of an equilateral triangle. One at a time, a small sphere is connected by a conducting wire with a large metal sphere that is charged. The center of the large sphere is in the straight line perpendicular to the equilateral triangle at its center, see the picture. As a result, the first small sphere acquires charge q1 and second charge q2 (q2 < q1). What is the charge that the third sphere (q3) will acquire?

The Attempt at a Solution

When the first sphere is connected to larger sphere,
charge on bigger sphere = Q-q1
Since the wire is conducting, the potential at the surfaces of bigger and smaller spheres will be the same.
\dfrac{k(Q-q_1)}{R} = \dfrac{k q_1}{r} \\<br /> Q = q_1 \left( 1+ \frac{1}{\mu} \right)
where μ=r/R

Similarly I get the relation q1=q2(1+μ)
Following a similar approach, I get
q_3 = q_1 - q_2 + \frac{q_2^2}{q_1}

But this is not the correct answer.

 

[BvU]

I read this moving story as follows:
Step 1: first sphere 1 is connected. (You work that out fine as far as I can see).
Step 2: Sphere 1 is disconnected and the wire is connected to sphere 2.
Step 3: Sphere 2 is disconnected and the wire is connected to sphere 3.

In that context I can't agree with "Similarly I get the relation q1=q2(1+μ)".

Furthermore, (Q-q1)=q2(1+μ) won't be correct either, because the potentials due to q1 at the big sphere and at q2 will be contributing differently. That's how l and d come in. I don't see a shortcut through a pile of hard work, so if you (or someone else) have a better idea...

 

[Tanya Sharma]

I think in this problem you have to assume that charge and potential of the bigger sphere do not change i.e they remain Q and V .

1. What is the potential of the bigger sphere ? Name it V
2. After the first sphere is connected to the bigger sphere what is the potential of the first sphere ? Name it V₁

 

[utkarshakash]

I think in this problem you have to assume that charge and potential of the bigger sphere do not change i.e they remain Q and V .

1. What is the potential of the bigger sphere ? Name it V
2. After the first sphere is connected to the bigger sphere what is the potential of the first sphere ? Name it V₁

If I assume this, all the small spheres would acquire same amount of charges equal to μQ. But this is not the case here as the question explicitly states that q2<q1.

 

[Tanya Sharma]

If I assume this, all the small spheres would acquire same amount of charges equal to μQ.

No...

Since the wire is conducting, the potential at the surfaces of bigger and smaller spheres will be the same.
\dfrac{k(Q-q_1)}{R} = \dfrac{k q_1}{r}

The potential of the first sphere(small) after connecting with bigger sphere is not kq₁/r .

Think carefully .The bigger sphere contributes to the potential of the smaller sphere .

Please reply to post#3.

 

[BvU]

the potentials due to q1 at the big sphere and at q2 will be contributing differently. That's how l and d come in.

And that's how q2 will be smaller than q1

 

[utkarshakash]

No...



The potential of the first sphere(small) after connecting with bigger sphere is not kq₁/r .

Think carefully .The bigger sphere contributes to the potential of the smaller sphere .

So,

1. What is the potential of the bigger sphere ? Name it V
2. After the first sphere is connected to the bigger sphere what is the potential of the first sphere ? Name it V1

V=\dfrac{kQ}{R} \\<br /> <br /> V_1 = \dfrac{kQ}{l-r} + \dfrac{kq_1}{r}\\ <br /> V_2 = \dfrac{kQ}{l-r} + \dfrac{kq_2}{r}\\<br /> V_3 = \dfrac{kQ}{l-r} + \dfrac{kq_3}{r}\\

 

[Tanya Sharma]

<br /> <br /> V_1 = \dfrac{kQ}{l-r} + \dfrac{kq_1}{r}\\ <br /> V_2 = \dfrac{kQ}{l-r} + \dfrac{kq_2}{r}\\<br /> V_3 = \dfrac{kQ}{l-r} + \dfrac{kq_3}{r}\\

This is incorrect .

Forget about second and third sphere for a moment.

Calculate potential at the center of smaller sphere ,not at the surface . Now what is V₁ ?

 

[utkarshakash]

This is incorrect .

Forget about second and third sphere for a moment.

Calculate potential at the center of smaller sphere ,not at the surface . Now what is V₁ ?

V_1 = \dfrac{kQ}{l} + \dfrac{kq_1}{r}

Is this correct?

 

[Tanya Sharma]

Good...

Now think carefully and write expression for V₂ .

 

[utkarshakash]

Good...

Now think carefully and write expression for V₂ .

kQ/l + kq2/r

 

[Tanya Sharma]

kQ/l + kq2/r

No...

Don't you think charge at the first sphere contributes to the potential of the second sphere ?

 

[utkarshakash]

No...

Don't you think charge at the first sphere contributes to the potential of the second sphere ?

OK.

V_2 = \dfrac{kQ}{l} + \dfrac{kq_2}{r} + \dfrac{kq_1}{d} \\<br /> V_3 = \dfrac{kQ}{l} + \dfrac{kq_3}{r} + \dfrac{k(q_1+q_2)}{d}

Is this still wrong?
[EDIT]
I got the correct answer. Thanks for helping.

 

[Saitama]

OK.

V_2 = \dfrac{kQ}{l} + \dfrac{kq_2}{r} + \dfrac{kq_1}{d} \\<br /> V_3 = \dfrac{kQ}{l} + \dfrac{kq_3}{r} + \dfrac{k(q_1+q_2)}{d}

Is this still wrong?
[EDIT]
I got the correct answer. Thanks for helping.

utkarshakash, can you please post the solution?

 

[utkarshakash]

utkarshakash, can you please post the solution?

V=\dfrac{kQ}{R} \\<br /> V_1 = \dfrac{kQ}{l} + \dfrac{kq_1}{r} \\<br /> V_2 = \dfrac{kQ}{l} + \dfrac{kq_2}{r} + \dfrac{kq_1}{d} \\<br /> V_3 = \dfrac{kQ}{l} + \dfrac{kq_3}{r} + \dfrac{k(q_1+q_2)}{d} \\<br />

V1=V2=V3=V

Equating V1 and V2, you can get the ratio r/d. Then, equate V1 and V3 and substitute the value of r/d derived earlier to get the final answer.

The correct answer is q3 = \dfrac{q_2^2}{q_1}

Hope this helps.

 

[Saitama]

V=\dfrac{kQ}{R} \\<br /> V_1 = \dfrac{kQ}{l} + \dfrac{kq_1}{r} \\<br /> V_2 = \dfrac{kQ}{l} + \dfrac{kq_2}{r} + \dfrac{kq_1}{d} \\<br /> V_3 = \dfrac{kQ}{l} + \dfrac{kq_3}{r} + \dfrac{k(q_1+q_2)}{d} \\<br />

V1=V2=V3=V

Equating V1 and V2, you can get the ratio r/d. Then, equate V1 and V3 and substitute the value of r/d derived earlier to get the final answer.

The correct answer is q3 = \dfrac{q_2^2}{q_1}

Hope this helps.

I am not sure if I get it but why don't you consider the potential due to three smaller spheres while writing down the expression for V?

 

[utkarshakash]

I am not sure if I get it but why don't you consider the potential due to three smaller spheres while writing down the expression for V?

Because initially the smaller spheres are uncharged and as suggested by Tanya, the potential of the bigger sphere remains unchanged. So, even if the spheres later acquire charges, they do not affect the initial potential of the bigger sphere which equals kQ/R.

 

[Saitama]

Because initially the smaller spheres are uncharged and as suggested by Tanya, the potential of the bigger sphere remains unchanged. So, even if the spheres later acquire charges, they do not affect the initial potential of the bigger sphere which equals kQ/R.

I still don't see it. The problem statement mentions nothing about the potential of bigger sphere remaining unchanged.

 

[utkarshakash]

I still don't see it. The problem statement mentions nothing about the potential of bigger sphere remaining unchanged.

I know the problem statement does not mention this. But approximating it to be constant throughout the process does give the correct answer.