What Determines the Point of Minimum Loudness in Speaker Interference?

AI Thread Summary
The discussion centers on determining the distance from speaker S1 where Hillary experiences minimum loudness due to destructive interference. The speed of sound is given as 343 m/s, with a frequency of 587 Hz, leading to a calculated wavelength of 0.584 m. The speaker separation of 2.78 m is significant because it influences the conditions for destructive interference, which occurs when the path difference between the sound waves from the two speakers is a half-integer multiple of the wavelength. To achieve minimum loudness, the distances from Hillary to each speaker must differ by half the wavelength. Understanding these concepts is crucial for solving interference problems in acoustics.
Student3.41
Messages
70
Reaction score
0

Homework Statement



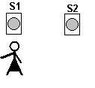
Hillary stands directly in front of speaker S1 and walks straight away (down on the page) from S1 as shown in the diagram.

What is the first distance (measured from S1) at which she will hear minimum loudness? Speed of sound is 343 m/s and the frequency of the sound is 587 Hz. The speakers are 2.78 m apart

Can someone explain what the significance of the speaker separation is in problems also??

Homework Equations





The Attempt at a Solution



Solved for Wave length = 0.584m, I then figured minimum loudness would be where constructive interference fisrt meets n=+/-1. So what do i do...
 

Attachments

  • Speakers_4.jpg
    Speakers_4.jpg
    2 KB · Views: 444
Physics news on Phys.org
Noone?, again.. I figured outthe beat question.
 
Minimum loudness will correspond to destructive interference, not constructive interference.

Compare Hillary's distance to S1, with Hillary's distance to S2. What must be true about those distances in order to have destructive interference? (Your textbook or class lecture notes should have something to say about this.)
 
Thread 'Collision of a bullet on a rod-string system: query'

Thread 'Collision of a bullet on a rod-string system: query'

In this question, I have a question. I am NOT trying to solve it, but it is just a conceptual question. Consider the point on the rod, which connects the string and the rod. My question: just before and after the collision, is ANGULAR momentum CONSERVED about this point? Lets call the point which connects the string and rod as P. Why am I asking this? : it is clear from the scenario that the point of concern, which connects the string and the rod, moves in a circular path due to the string...
View full post »
Thread 'A cylinder connected to a hanged mass'

Thread 'A cylinder connected to a hanged mass'

Let's declare that for the cylinder, mass = M = 10 kg Radius = R = 4 m For the wall and the floor, Friction coeff = ##\mu## = 0.5 For the hanging mass, mass = m = 11 kg First, we divide the force according to their respective plane (x and y thing, correct me if I'm wrong) and according to which, cylinder or the hanging mass, they're working on. Force on the hanging mass $$mg - T = ma$$ Force(Cylinder) on y $$N_f + f_w - Mg = 0$$ Force(Cylinder) on x $$T + f_f - N_w = Ma$$ There's also...
View full post »

Similar threads

Audio interference of sound waves from two speakers
Replies
19
Views
4K
Sound Interference Problem -- Observer moving between two speakers
Replies
3
Views
4K
What is the Maximum Wavelength for Constructive Interference of Sound Waves?
Replies
3
Views
3K
Sound Wave Interference and Finding the Path Differences with Diagrams
Replies
20
Views
5K
Sound wave Interference from Two Speakers
Replies
3
Views
4K
Constructive interference with sound -- word problem
Replies
15
Views
3K
Destructive vs Constructive interference
Replies
2
Views
4K
Destructive interference and constructive interference
Replies
3
Views
3K
Question on destructive and constructive interference
Replies
6
Views
3K
How Far Must Point P Be from Speaker A for Constructive Interference at 400 Hz?
Replies
1
Views
1K

Hot Threads

Recent Insights

Back
Top