baylorbelle
- 14
- 0
You are designing exercise equiptment to operate as shown in the figure:
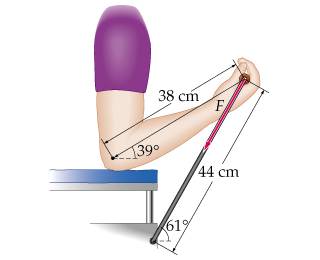 where a person pulls upward on an elastic stretched length of .31m. If you would like the torque about the elbow joint to be 81 N*m in the position shown, what force constant, k, is required for the cord?
where a person pulls upward on an elastic stretched length of .31m. If you would like the torque about the elbow joint to be 81 N*m in the position shown, what force constant, k, is required for the cord?
::: okay, so since this picture has so many angles, i figured the first thing to do was to break each part down into its x and y components and create two separate pictures:
: picture 1 is the arm, hypotenuse (length of arm) at 38 cm, x-axis = 38 cos (39)=10.1 cm, and y-axis = 38 sin(39)=36.6 cm.
: picture 2 is the cord, hypotenuse (length of stretched cord) 44cm, x-axis: 44cos(61)=11.4 cm, y-axis=44sin(61)=42.5cm.
I think that for the cord, it starts in potential energy of c=.5kx2 and ends in both potential and kinetic (.5mv2) energy.
I also know that torque= rF sin theta
However, I don't quite understand how I'm supposed to set it up from here. any advice on getting this one started?
::: okay, so since this picture has so many angles, i figured the first thing to do was to break each part down into its x and y components and create two separate pictures:
: picture 1 is the arm, hypotenuse (length of arm) at 38 cm, x-axis = 38 cos (39)=10.1 cm, and y-axis = 38 sin(39)=36.6 cm.
: picture 2 is the cord, hypotenuse (length of stretched cord) 44cm, x-axis: 44cos(61)=11.4 cm, y-axis=44sin(61)=42.5cm.
I think that for the cord, it starts in potential energy of c=.5kx2 and ends in both potential and kinetic (.5mv2) energy.
I also know that torque= rF sin theta
However, I don't quite understand how I'm supposed to set it up from here. any advice on getting this one started?