What formula is most suitable?

[solarmidnightrose]

Homework Statement

I've been trying to calculate the rotational inertia of this rotating gondola on this ride at this theme park.

However, they do not directly give me a specific formula to use-because with different objects, there are different formulae that you use to determine the rotational inertia of an object

mass of gondola = 6 tonne (6000kg)
radius = 3m


I will attach a picture of what it looks like

Relevant Equations

I have attached a picture of different possible formulae's

Picture of gondola:

Formulae:

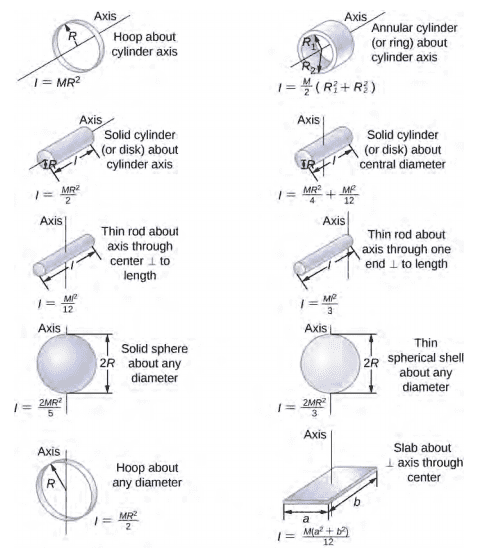
Initially, I used the equation: I=mr^2

I=(6000)x(3)^2​

T=54,000kgm^2

(but apparently this is incorrect)​

​

So, basically, I don't know which formula would suit best for the gondola (the picture above). I would consider the gondola a hollow object as the mass is concentrated on the outer edges.​

 

[haruspex]

which formula would suit best for the gondola

The key question is what axis is it rotating about? I am unfamiliar with this equipment, but it looks like it swings like a pendulum from somewhere up above. If so, you need to know how high that is. You would then apply the "hoop about a diameter" formula, and using the parallel axis theorem add a term mh² where h is the height of the axis.

 

[tkyoung75]

The assumption that all the weight is in a ring is massive.
It will affect the torque required to drive the system, and the velocity of the driven system.
Furthermore, If all the mass were in the ring it would have to be very precisely balanced.

 

[solarmidnightrose]

The key question is what axis is it rotating about? I am unfamiliar with this equipment, but it looks like it swings like a pendulum from somewhere up above.

Yes, you're assumption/idea of the ride is correct :) (sorry, I should have provided a video)
video: (I believe only the first 10 seconds is enough)

Anyways, if I take into consideration the axis that the gondola is rotating about then that would be the arm/pendulum-tube that the gondola is attached to? (I've circled this part in blue) Is this correct?-I just want some confirmation please.

If so, you need to know how high that is. You would then apply the "hoop about a diameter" formula, and using the parallel axis theorem add a term mh² where h is the height of the axis.

The length of the pendulum tube is 15m.
Would it be alright to say that the 'height' of the axis (i.e. the pendulum tube) is 15m?

If I use the "hoop about a diameter formula", then I would:

1. substitute the mass/radius of the gondola into the "hoop about a diamter formula"
2. add the (mh^2) to the above answer.

My attempt at your suggestion:

@haruspex , am I doing this correctly? have I substituted the correct values into the formula? have I even done the right thing by adding "mh^2" to "hoop about a diameter formula"?

Thanks for your help/input; very kind.

 

[solarmidnightrose]

The assumption that all the weight is in a ring is massive.

Thanks for that, @tkyoung75 .
My teacher was telling us that for this report that many assumptions would have to be made in order to help explain the physics concepts behind these rides at theme parks.

So, since this rotational inertia of this gondola must be HUGE, then is that why an external torque provider such as a motor would be used in rides such as this to get it spinning in the first place? If so, then that would really help my report.

Thanks for your help :)

 

[Nugatory]

So, basically, I don't know which formula would suit best for the gondola (the picture above).

The formulas you posted are all different special cases of the general and always applicable $I=\int \rho(\vec{r})r^2dV$ (and it would be a good exercise to see if you can derive some of them from this general formula).

You'll solve this problem by making a reasonable assumption about what $\rho$ might be, identifying the axis of rotation, and then evaluating the integral.

 

[solarmidnightrose]

The formulas you posted are all different special cases of the general and always applicable $I=\int \rho(\vec{r})r^2dV$ (and it would be a good exercise to see if you can derive some of them from this general formula).

You'll solve this problem by making a reasonable assumption about what $\rho$ might be, identifying the axis of rotation, and then evaluating the integral.

I'm sorry, but my teenage brain is screaming/crying looking at that integral.

Also, what is this 'roh' in the integral?

I apologise @Nugatory if I come off as rude, but this is something that I haven't been taught yet. Do you think it's possible to learn all this derivative-stuff/integration in a couple of hours (6hrs max)? If yes, then "yay!".

If no, then I'm screwed.

 

[tkyoung75]

What do you have to do to change the direction?

So, since this rotational inertia of this gondola must be HUGE, then is that why an external torque provider such as a motor would be used in rides such as this to get it spinning in the first place? If so, then that would really help my report.

This about Newtons laws of motion.

 

[solarmidnightrose]

What do you have to do to change the direction?

Apply an unbalanced torque to cause it to accelerate angularly-i.e. spin/rotate. (Newtons II Law).

This about Newtons laws of motion.

Oh okay, that's cool.

Thanks-I believe I get this idea of rotational inertia better now.

It's just that I have a hard time trying to actually calculate the rotational inertia (I guess you could say I'm not very mathematically strong).

 

[tkyoung75]

Do you know the basic formula for inertia?

 

[solarmidnightrose]

Do you know the basic formula for inertia?

Is it I=mr^2? (rotational inertia)

 

[tkyoung75]

That is the one I had in mind. Do you know how to add them together, if you have a mass in the centre and a mass on the outside?

 

[solarmidnightrose]

That is the one I had in mind. Do you know how to add them together, if you have a mass in the centre and a mass on the outside?

No, I have no idea.

But I have a feeling its got something to do with Centre of Mass? (which is something I can do-calculate the CoM; but I don't know if that's relevant).

An earlier post mentioned something about the Parallel Axis Theorem-(but I have never come across this before) and I am not sure how important I need to know this in order to find the rotational inertia of the gondola in this ride.

 

[haruspex]

Yes, you're assumption/idea of the ride is correct :) (sorry, I should have provided a video)
video: (I believe only the first 10 seconds is enough)

Anyways, if I take into consideration the axis that the gondola is rotating about then that would be the arm/pendulum-tube that the gondola is attached to? (I've circled this part in blue) Is this correct?-I just want some confirmation please.
View attachment 244611

The length of the pendulum tube is 15m.
Would it be alright to say that the 'height' of the axis (i.e. the pendulum tube) is 15m?

If I use the "hoop about a diameter formula", then I would:

1. substitute the mass/radius of the gondola into the "hoop about a diamter formula"
2. add the (mh^2) to the above answer.

My attempt at your suggestion:
View attachment 244612
@haruspex , am I doing this correctly? have I substituted the correct values into the formula? have I even done the right thing by adding "mh^2" to "hoop about a diameter formula"?

Thanks for your help/input; very kind.

Yes, that looks about right... except, watching the video to the end I see there is a long section of tube above the axle, possibly with a counterweight on the end. This could easily add 50%; hard to know without more data.

Also I see there is some rotation about the tube axis, but this is small by comparison and does not add to the above since it relates to an orthogonal rotation.

 

[haruspex]

Parallel Axis Theorem-(but I have never come across this before)

So Google it.

 

[tkyoung75]

Well if you had two masses each traveling in the same direction and they hit a wall at the same speed at the same with force F, what would the total force be?

 

[solarmidnightrose]

Yes, that looks about right... except, watching the video to the end I see there is a long section of tube above the axle, possibly with a counterweight on the end. This could easily add 50%; hard to know without more data.

Also I see there is some rotation about the tube axis, but this is small by comparison and does not add to the above since it relates to an orthogonal rotation.

I am so thankful for your help

So Google it.

haha, yeah I did.