What Happens to Momentum and Energy During an Inelastic Collision?

[beeohbee]

Homework Statement

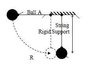
Each equal ball shown in figure 1 is suspended on a separate inextensible string of equal length R. The strings are attached to a rigid support and the attachment points are separated by a distance equal to the diameter of the balls. Both balls are initially stationary in the position illustrated. Ball B is hanging on a vertical cable and ball A is held with the string taught and horizontal. When ball A is released its motion is frictionless until it collides with ball B.

If at the instant after collision, both balls move with the same velocity, determine expressions for:-

a). The velocity immediately following impact.
b). The proportion of energy lost during impact.

If there were no losses during impact determine:-
c). Expressions giving the velocity of each ball immediately following impact.

Homework Equations

PE = m.g.h
KE = \frac{1}{2}.m.v²
p = m.v

The Attempt at a Solution

I'm assuming that for a and b, the collision is inelastic and the balls move together, which is why they have the same velocity but this is as far as I can get.

For c, I've got:
Potential energy completely turns to kinetic energy at the point of collision as it's the lowest point and KE=PE. Therefore, m.g.h = \frac{1}{2}.m.v².
From this, v = \sqrt{2gh} and I assume that as this is an elastic collision, this is transferred to Ball B and Ball A remains stationary.

Any help to get me going on section a and b would be helpful and I hope someone can tell me I'm along the right lines with section c as well!

Thanks

 

[Doc Al]

I'm assuming that for a and b, the collision is inelastic and the balls move together, which is why they have the same velocity but this is as far as I can get.

Hint for all three: What's conserved in any collision?

 

[Bacat]

I'll make it a little easier for you. For any collision problem you need to consider the momentum of the system before and after collision. Remember that momentum is the mass times the velocity:

p = mv

For a perfectly inelastic collision, the momentum of the two objects before the collision should equal the momentum of the new object (the balls stuck together) after the collision.

Can you write an expression that takes this into account?

 

[beeohbee]

OK, so if v = \sqrt{2.g.h} at collision,
Ball A's momentum =m.\sqrt{2.g.h}
Ball B has no momentum, so the total system momentum = =m.\sqrt{2.g.h}
Therefore m.\sqrt{2.g.h} /2m = the velocity after the collision
V = \sqrt{2.g.h} /m

For b) Putting the new velocity back into the kinetic energy equation:
E_k = \frac{1}{2}.m.(\sqrt{2.g.h})² / m
Therefore, the new kinetic energy is \frac{g.h}{m}
So the proportion of kinetic energy lost is m.g.h - \frac{g.h}{m}

Are my answers to a) b) and c) now correct? This seems right to me

 

[Doc Al]

OK, so if v = \sqrt{2.g.h} at collision,
Ball A's momentum =m.\sqrt{2.g.h}
Ball B has no momentum, so the total system momentum = =m.\sqrt{2.g.h}

Good.

Therefore m.\sqrt{2.g.h} /2m = the velocity after the collision

Good.

V = \sqrt{2.g.h} /m

Oops... redo this more carefully.

(Tip: Checking the units of your expressions will catch many errors.)

 

[beeohbee]

Oops... redo this more carefully.

(Tip: Checking the units of your expressions will catch many errors.)

By squaring both sides it works out as:

V = \sqrt{g.h}
I'm pretty sure the units cancel here.
This means that for b) :
The new kinetic energy is \frac{1}{2}.m.g.h
As the kinetic energy changed from m.g.h to \frac{1}{2}.m.g.h, the proportion of energy lost during impact was half.

 

[Doc Al]

By squaring both sides it works out as:

V = \sqrt{g.h}

Still not quite right. You had the correct expression before, you just messed up the division:

v = m*√(2gh) /2m = √(2gh) /2 ≠ √(gh)

note: (√2)/2 = 1/√2 ≠ 1 (The 2 doesn't cancel.)

I'm pretty sure the units cancel here.

Yes, the units are fine now. Progress!

But redo it one more time with the correct velocity.

 

[beeohbee]

I've got it now, I couldn't get my head around the difference between m+m and 2 m on the bottom. With the new velocity I get the kinetic energy after the collision to be:
E_k=\frac{1}{2}.m.\frac{2.g.h}{4}
Therefore, E_k=\frac{1}{4}.m.g.h
So the proportion of E_k lost is \frac{3}{4}

Thanks for all your help, couldn't have done it without you guys

 

[Doc Al]

I've got it now, I couldn't get my head around the difference between m+m and 2 m on the bottom. With the new velocity I get the kinetic energy after the collision to be:
E_k=\frac{1}{2}.m.\frac{2.g.h}{4}
Therefore, E_k=\frac{1}{4}.m.g.h

Don't forget that there are two masses. What's the total KE after the collision?