orlan2r
- 31
- 0
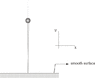
We have the structure show in figure (ball mass m joined a dipstick mass is negligible). If the structure start to move of the position showed, find the angle between the dipstick and x-axis when the force in the dipstick es null (don't exists friction).
I've analized this problem but I arrived to a contradiction.
PD: I'm sorry for grammatical errors (I'm from Peru).
I've analized this problem but I arrived to a contradiction.
PD: I'm sorry for grammatical errors (I'm from Peru).