Prateek Kumar Jain
- 8
- 2
As per the Gauss Law , Net Flux Electric Field through a closed Surface (Gaussian Surface) is zero if no charge is enclosed.
As per the definition of the Electrical Flux = Electrical Field Intensity dot product Area Vector i.e. Closed Integral of E.S
If Electrical Flux is zero then as per the definition of Electric Flux above , Electric Field intensity through the Gaussian Surface should also be zero, which is not so as shown in the figure below
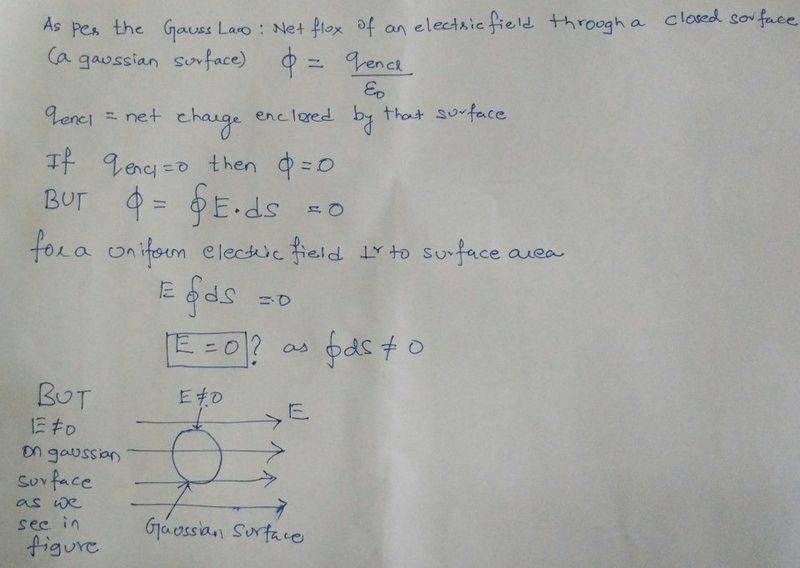
Please clarify why the two results are opposite and which one is correct.
As per the definition of the Electrical Flux = Electrical Field Intensity dot product Area Vector i.e. Closed Integral of E.S
If Electrical Flux is zero then as per the definition of Electric Flux above , Electric Field intensity through the Gaussian Surface should also be zero, which is not so as shown in the figure below
Please clarify why the two results are opposite and which one is correct.