What is Returning Loop of Rogowski Coil?

[endiewibowo]

I read on a source from a paper from John D. Ramboz that explains:

The incremental pitch-advancement of the coil's helical winding sums over its circumferential length to create an undesirable one-turn loop normal to the axis of the coil (the plane of this loop is parallel to the surface of the paper). Any magnetic flux normal to this loop (in or out the paper surface) induces an error voltage into the coil's output...

...To compensate for this undesirable one-turn loop, another one-turn loop is place inside of the helical winding in the opposite direction to that of the pitch advancement. It is connected electrically in series with the coil output. In theory, a compensation voltage is induced equal and opposite to that induced in the pitch-advancement loop. This, under certain flux condition, cancels the errors caused by the one turn pitch loop when both are exposed to the unwanted flux.

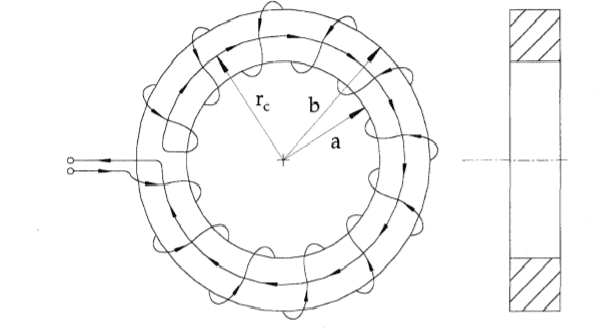
(The arrows indicate the direction of winding)

What I don't understand are:

1. What does pitch-advancement mean? I know that 'pitch' in this case means the distance between the windings. But I don't understand the sentence:
The incremental pitch-advancement of the coil's helical winding sums over its circumferential length...

2. How does this pitch-advancement create extra one-turn loop normal to the axis of the coil. I cannot visualize it at all.

I hope somebody can help me to understand this. Thank you.

 

[sophiecentaur]

A single loop around an AC current carrying cable will produce a small emf due to a field in a plane, normal to the cable. The Rogowski coil attempts to add the emfs from a large number of turns BUT:
Affaics, each of the turns of wire around the helix has a 'forward' component, around the loop. The effect of each of these 'pitch advancements' is a small emf when there is any changing magnetic field that's not in the plane of the torus. The current flowing in the cable produces only a field in the plane of the torus and this is what you want to measure. Spurious changing fields, not in this plane will produce an error reading but it can be canceled out by the action of the single loop that returns the current back to the connector. It's a sort of bifilar effect in which one induced emf cancels another. I guess this could be useful if another cable passes close to and crosses over the cable being measured.
Dead clever and I had never come across that before (not being a Power Engineer)

 

[endiewibowo]

Hello @sophiecentaur , thanks for replying.

I still don't understand how this 'forward' component can produce small emf when there is any changing magnetic field that's not in the plane of torus. If the returning loop is used to compensate this, it means that the magnetic flux produced by this 'forward' component is parallel to the magnetic flux produced by returning loop (in opposite direction) and normal to the plane of torus, right? But I still can't imagine how this 'forward' component can produce magnetic flux that is normal to the plane of torus. Could you provide me a sketch of the field lines?

Thak you so much.

 

[sophiecentaur]

how this 'forward' component can produce magnetic flux that is normal to the plane of torus.

I notice you are addressing this problem the other way round - a valid approach, if it helps with understanding!
The additional effective, single, turn of wire is the result of adding all the (component) parts of the coil that are not parallel with the cable, it is in the plane of the induced field from the cable and parallel with it, all the way round. It is just one loop, however many turns are in the solenoid. So there will be no induced emf from the cable. Fields that are out of the plane will have an effect, though. The additional return loop will cancel this effect because the emf is in the opposite sense..
I can't easily give you a sketch (beyond the call of duty, I'm afraid ) Just draw a single circle through the centre of the torus. This represents the field from the cable. It is parallel with the 'virtual' loop and there is no induction. Draw a circle (field from somewhere else) at an angle and there is a component that can induce an emf.
It's is true to say that the rejection of off axis fields in only complete for fields that are parallel with the cable because any other field will still induce an emf in the other components of the solenoid wire. Better than nothing and its maximum sensitivity is to the current flowing in the cable.

 

[endiewibowo]

@sophiecentaur

Ah yes! Now I understand it. Thank you very much! I really appreciate your help.

So, suppose I don't make a single returning wire but make windings in opposite direction instead. It will reject off axis fields more, right?

 

[sophiecentaur]

I think it's cleverer than that. Having a single coil, not going back on itself, will discriminate against fields around parallel cables. If you just had a large number of turns, all bunched up on one side of the cable or a two direction solenoid as you suggest, it would be just as sensitive as the toroidal coil but it would pick up from all nearby cables. That's my present way of thinking, anyhow. Does it make sense to you?

 

[endiewibowo]

@sophiecentaur

But wait, it's just crossed my mind. I think that the sum of every component of the helix over the torus' circumferential length is normal to the cable. I sketched it and it makes sense. So the helix are treated as one single loop and the flux of that loop is parallel to the cable.

So yes, in order to compensate spurious field (normal to the torus), we need one loop returning back. However, since the torus has much bigger cross sectional diameter (as big as the helix itself) than the returning loop (as big as the diameter of wire), maybe the compensation is not that effective.

But if I make opposite windings, it means that I have 2 torus which has opposite direction of current with the same diameter. So I think it will be more effective to compensate spurious field. What do you think?

 

[sophiecentaur]

I think the single return loop is directly equivalent because some of the torus has smaller distance fro the cable.
I agree about the return torus idea BT why isn't it done that way, always, I wonder? EXPERTS ?!

 

[endiewibowo]

Maybe it will be more complicated to build that way. I read from that paper (John D. Ramboz), he said that the undesired one-loop has much bigger diameter (the helix itself) compared to the returning loop. I guess he treats the torus as one big loop but I'm not really sure why and how does his theory work.

 

[John D Ramboz]

In response to Message #9 of Feb 12, it is the area of the "undesired one-turn loop" compared to the sum of the areas of the coil turns that is to be considered. The feature that distinguishes a Rogowski coil from a similar mutual inductor is indeed the addition of the "pitch-advancement compensation", or "PAC" abbreviated for purposes of this discussion. For example, for a coil having a mean diameter of 5 in., a square cross sections turn area of 1 sq. in. and 130 turns, the one-turn-loop has an area of approximately 19.6 sq. in. The sum of the turns-areas for 130 turns would be 130 sq. in. If the field from an adjacent return conductor were next to the outer edge of the coil and normal to the axis of the coil, the maximum error would be approximately 15% for a coil not having PAC. Granted, this is an unlikely geometry for the return conductor, but it is useful to demonstrate a worse-case situation.

It (PAC) is simple in concept, yet continues to elude a clear understanding. Many of the discussions regarding Rogowski coils only consider the very basic coil and current-conducting bus in very simple geometry conditions; namely that the coil is centered on and is normal to single bus. Further, seldom considered is the fact that any other nearby conductors are present, for example the return conductor of the circuit. Real life situations entail coils that are not centered, are not at right-angles to the bus, and importantly that other conductors are nearby. This can be even more complex if one is considering, for example the line current on a 3-phase circuit with adjacent bundle conductors. Each of these situations can be the source of significant error contributions coils, even those having PAC.

For coils used for many routine current measurements, accuracies of a few percent are easily achievable. However, for applications such reference standards do require much better accuracy, say in the order of a few tenths of a percent. Only very high quality Rogowski coils can reliably achieve this.

Hope this contributes to some better understanding and appreciation regarding Rogowski coils.

John D. Ramboz