What is the Correct Formula for Calculating the Velocity of Saturn's Rings?

[nmsurobert]

I'm setting up a lab for my class and I've found this equation, but I can't find where a constant value is coming from.

"...the speed of rotation of the rings is related to their radius (from the center of Saturn) by the following equation:

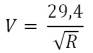
where R is the distance from the center of Saturn to the ring in multiples of the radius of Saturn (R = 1 corresponds to a distance of 60.268 km)."

The only relation I can find between 29.4 and Saturn, is that it take 29.4 years for Saturn to complete an orbit. I don't think that has anything to do with this equation though.

Can anyone here explain to me where 29.4 is coming from?

 

[Drakkith]

Hmmm. I think it has something to do with centripetal acceleration, but I'm not certain.

 

[Bandersnatch]

Since each ring particle follows a Keplerian orbit, this should be just the formula for circular orbital velocity, with constants folded into one. I.e. for a small orbiting particle:
$V_o=\sqrt{\frac{GM}{R}}$
The numerical constant is then just the orbital speed at the planet's surface (let us know if you can't see how to get there).
However, there's something wonky in the state of Denmark. If you calculate it for Saturn's mass and 1 orbital radius, you should get approx. 25 km/s, not 29.4.
The only two sources for the formula I could find is some amateur astronomer's blog that only mentions 'bibliography', and the SpaceMath website: https://spacemath.gsfc.nasa.gov/weekly/10Page28.pdf
I went over the solutions to the problems they gave, and the numbers didn't match for P1 and 2. Why that is became clear with problem 3, where it turns out the 29.4 is just a typo. The correct value (which they were actually using) is 24.9 - and that matches what you get from the orbital velocity formula.

So, yeah. Don't use it. Use:
$V=\frac{24.9}{\sqrt{R}}$
Again, 24.9 km/s is the orbital velocity in circular orbit at Saturn's surface (aka first cosmic velocity).

 

[nmsurobert]

Since each ring particle follows a Keplerian orbit, this should be just the formula for circular orbital velocity, with constants folded into one. I.e. for a small orbiting particle:
$V_o=\sqrt{\frac{GM}{R}}$
The numerical constant is then just the orbital speed at the planet's surface (let us know if you can't see how to get there).
However, there's something wonky in the state of Denmark. If you calculate it for Saturn's mass and 1 orbital radius, you should get approx. 25 km/s, not 29.4.
The only two sources for the formula I could find is some amateur astronomer's blog that only mentions 'bibliography', and the SpaceMath website: https://spacemath.gsfc.nasa.gov/weekly/10Page28.pdf
I went over the solutions to the problems they gave, and the numbers didn't match for P1 and 2. Why that is became clear with problem 3, where it turns out the 29.4 is just a typo. The correct value (which they were actually using) is 24.9 - and that matches what you get from the orbital velocity formula.

So, yeah. Don't use it. Use:
$V=\frac{24.9}{\sqrt{R}}$
Again, 24.9 km/s is the orbital velocity in circular orbit at Saturn's surface (aka first cosmic velocity).

Awesome! Thank you. After reading your explanation I couldn't figure out where the 25 was coming from. I kept getting 25000... meters. Duh.

Thanks again!