Tiiba
- 53
- 0
I did this three times, and always come up with utter nonsense.
What is the derivative of 4x(16-x^2)^0.5?
(Root of (16 minus x-squared) by 4x.) What are its zilches? How did you calculate that?
This derivative is part of the solution to this problem: "What are the dimentions of the largest rectangle (by area) inscribable in a circle with radius 4?"
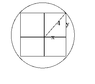
I drew the circle and the square (see attachment), divided the square into four parts, drew a diagonal through one, and called it a hypotenuse, which is equal to 4. X and y are the sides of the mini squares. A = 4xy (since there are 4 mini-squares). Then I used Pythagoras to come up with that equation above. But I can't differentiate it now...
The final answer is supposed to be 32 square units.
What is the derivative of 4x(16-x^2)^0.5?
(Root of (16 minus x-squared) by 4x.) What are its zilches? How did you calculate that?
This derivative is part of the solution to this problem: "What are the dimentions of the largest rectangle (by area) inscribable in a circle with radius 4?"
I drew the circle and the square (see attachment), divided the square into four parts, drew a diagonal through one, and called it a hypotenuse, which is equal to 4. X and y are the sides of the mini squares. A = 4xy (since there are 4 mini-squares). Then I used Pythagoras to come up with that equation above. But I can't differentiate it now...
The final answer is supposed to be 32 square units.