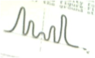What is the energy of this harmonic oscillator state?

[szamito]

[SOLVED] Find the energy of oscillator

Homework Statement

The Probability density for the states of a harmonic oscillator is shown in the figure. Find the energy of the oscillator in this state if the ground state energy is 2 [eV].

Homework Equations

E_n=(n^2)*E_1

The Attempt at a Solution

n=5 then E_5=5^2*2 eV=50 eV

 

[monish]

This looks wrong to me. The spacing of the energy levels of the harmonic oscillator doesn't go as n-squared, rather it goes as n. I think. Also, the sketch as shown appears to me to be the 9th level, not the 5th. (Try drawing out the first three or four levels to see how it goes.) So I would put this state at 18 eV.