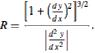Natus Homonymus
- 5
- 0
I understand that the centripetal force on an object of mass 'm' is (mv2)/r
However, isn't this for an object going around in a circle? Suppose I have a curve (0.0033x2+−1.0038x+98.2331). What would be the fastest speed around this curve on the bounds x ->
Please note that we would (obviously) have to take friction into account. Any help or methods/techniques to help me solve this would be greatly appreciated.
However, isn't this for an object going around in a circle? Suppose I have a curve (0.0033x2+−1.0038x+98.2331). What would be the fastest speed around this curve on the bounds x ->
Please note that we would (obviously) have to take friction into account. Any help or methods/techniques to help me solve this would be greatly appreciated.