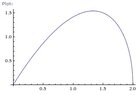
I was reading that the cone must be inscribed within a sphere, because you stated the cone was confined. And so I find the lateral surface area of the cone is maximized when the height of the cone is 4/3 times the radius of the sphere, and minimized at h=0 and h = 2R, as you can see from this plot (where I have let R=1):
View attachment 1886
However, had I really been paying attention before, I would have noticed that given the stated answer, the sphere must be in fact circumscribed by the cone.
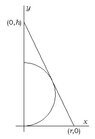
So, if we consider the cross-section of the two objects through their centers, there the center of the base of the cone is at the origin of our coordinate system, we find the slant height of the cone will lie along the line:
$$y=-\frac{h}{r}x+h$$
Now, this slant height will be tangent to the circle (representing the sphere of radius $R$):
$$x^2+(y-R)^2=R^2$$
So, what we may do is then substitute for $y$, and then require the discriminant of the resulting quadratic in $x$ to be zero. You should be able to use this to show:
$$r^2=\frac{hR^2}{h-2R}$$
Substituting this into the objective function (the lateral surface $S$ of the cone) you should be able to show that:
$$S(h)=\frac{\pi hR(h-R)}{h-2R}$$
Differentiating this with respect to $h$, and equating the result to zero, you should find this implies:
$$h^2-4Rh+2R^2=0$$
And from this, discarding the negative root because we require $2R<h$, we then find:
$$h=\left(2+\sqrt{2} \right)R$$
Now, at each step where I state "you should be able to show..." this is your cue to do just that. I have merely provided the outline of the steps that can be taken to get the desired result. I encourage you to work through the algebra and calculus and will be happy to assist if you get stuck, as I have worked out each step. I would just ask that you show what you did leading up to where you are stuck if this happens.