mathlearn
- 331
- 0
View attachment 5910
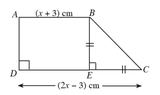
In the trapezium ABCD shown in the figure, AB = (x + 3) cm, DC = (2x − 3) cm and BE = EC. If the area of the trapezium is 15 cm2, find the length of DC to the nearest first decimal place.
Take $\sqrt{19}$ = $4.36$
Have I done correctly,
Okay first we know that area of a trapezium
$15 = \dfrac{((x+3)+(2x-3))h}{2}$
$h=(2x-3) -(x+3)$ $h=2x-3 -1(x+3)$
$h=2x-3 -x-3$
$h=x-3 -3$
$h=x-6$
, Correct ?
Many Thanks :)
In the trapezium ABCD shown in the figure, AB = (x + 3) cm, DC = (2x − 3) cm and BE = EC. If the area of the trapezium is 15 cm2, find the length of DC to the nearest first decimal place.
Take $\sqrt{19}$ = $4.36$
Have I done correctly,
Okay first we know that area of a trapezium
$15 = \dfrac{((x+3)+(2x-3))h}{2}$
$h=(2x-3) -(x+3)$ $h=2x-3 -1(x+3)$
$h=2x-3 -x-3$
$h=x-3 -3$
$h=x-6$
, Correct ?
Many Thanks :)
Attachments
Last edited: