What Is the Lowest Frequency for a Standing Wave in a Compound Wire?

[Stealth849]

Homework Statement

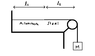
An aluminum wire of length l₁ = 60cm, cross section area 1.00 x 10^-2cm², and density 2.60g/cm³, is joined to a steel wire of density 7.8g/cm³ and same cross sectional area. The compound wire loaded with a block of mass m = 10kg is arranged as shown so that the distance l₂from the joint to the supporting pulley is 86.6cm. Transverse waves are set up in the wire using an external source of variable frequency. A node is located at the pulley.

a) find the lowest frequency of excitation for which a standing wave is observed to have a node at the joint.

b) How many nodes are observed at this frequency?

Homework Equations

f = v/λ = nv/2l

ρ = m/V

v = sqrt(F_T/μ)

The Attempt at a Solution

Not too sure where to begin on this one. When it asks for the lowest frequency of excitation, I expect that means the second harmonic, because that would leave a node at the joint with the lowest frequency.

So knowing the densities of the wires, I can get v where

F_T = μv²
F_T = mg = 98N

μ = m/l = ρV/l = ρA where A represents the cross sectional area.

so μ₁ = 2600*0.0001 = 0.26

μ₂ = 7800*0.0001 = 0.78

v₁ = sqrt(98/0.26) = 19.4m/s
v₂ = sqrt(98/0.78) = 11.2m/s

so f = nv/2l

where n = 2 for the second harmonic

f₁ = 2*0.26/(2*0.6) = 0.43Hz

f₂ = 2*0.78/(2*0.866) = 0.90Hz

No idea if I'm approaching this correctly, due to the idea of reflection of waves at the joint.. Say a wave does reflect at the joint and a portion of it is sent back to the source, there would be a lot more waves thus being a much higher harmonic - not the second.

Any and all help appreciated. Thanks!

 

[Simon Bridge]

When it asks for the lowest frequency of excitation, I expect that means the second harmonic

er ... that would be the case if the wave-speed is the same in each section of wire.

Think in terms of the modes in each section of wire, if the sections were separate.

 

[Stealth849]

Okay.. So if I know that

nv/2l = f

and am treating each section separately, except for the fact that frequency must be the same for each section, could I say that

nv₁/2l₁ = mv₂/2l₂

essentially setting frequency equal to frequency, but being able to solve for the number of nodes, or at least a ratio of nodes...?

as in

n/m = l₁*v₂/l₂*v₁

Thanks for the reply :)

 

[Simon Bridge]

Well done.
The other approach was to solve the wave equation directly :)

 

[Stealth849]

Thanks!

I don't see how I could solve the wave equation directly as you said, however. Can you define what you mean by wave equation?

Using what I mentioned previously...

n/m = l1*v2/l2*v1
n/m = 0.6*11.2/(0.866*19.4) which is roughly 2/5

So this means that the aluminum section, l_1, has 2 nodes and the steel section has 5 nodes, yes?

and frequency can be calculated by either side,

f = nv/2l
f = 19.4/0.6 = 32.3Hz
f = 5*11.2/2*0.866 = 32.3Hz

and the total number of nodes will be 2 + 5 = 7?

 

[Simon Bridge]

Wave equation:
$$\frac{\partial^2}{\partial x^2}y(x,y) = \frac{1}{c^2}\frac{\partial^2}{\partial t^2}y(x,t)$$ ... in your case, the wave-speed, c, depends on x so it will need some modification.

Since $c=f\lambda$, which will have the longer wavelength for the same frequency? The fast one or the slow one?

 

[Stealth849]

Well, if c is proportional to to wavelength, the faster one should have the longer wavelength...no?

How did you get to that wave equation? Or is that a standard model for a wave?

 

[Simon Bridge]

Well, if c is proportional to to wavelength, the faster one should have the longer wavelength...no?

That's how you check your answers make sense :)

How did you get to that wave equation? Or is that a standard model for a wave?

http://en.wikipedia.org/wiki/Wave_equation
Deriving the 1D case from Hook's Law used to be a college-level exercise...

 

[Stealth849]

Deriving the 1D case from Hook's Law used to be a college-level exercise...

I'm sure it still is... Looking forward to learning it eventually when college rolls around. :)

Do you mind giving me a quick introduction to how that equation works...?

 

[Simon Bridge]

It's a second order partial differential equation - if we consider y(x,t) to be a transverse displacement of a point on the string at position x along the string, then it says that the way a point on a string accelerates (the RHS) depends on how the string around that point is curved (the LHS).

Any wave has to be consistent with that equation, and the external "boundary conditions" - like being fixed at both ends and having a node in a particular place.