What is the Magnetic Field Between Parallel Plate Electrodes?

[airbuzz]

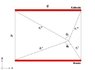
I have two parallel plate electrodes in which flows a determined current J. I found that the magnetic field between the two electrodes is:

B_z (y,z)=\frac{\mu J}{2\pi d}(\vartheta_1+\vartheta_2}

(see attached figure)

This comes form the field generated by a plate that is:

B_z (y,z)=\frac{\mu J}{2\pi d}\vartheta

Does anybody knows from where come this formula and how to demonstrate it??

I´m just fighting against Maxwell´s equations, but they are winning...

 

[eys_physics]

Can you explain \vartheta[\tex] means?

 

[airbuzz]

it is a TeX command to write theta in that way.

\theta \Rightarrow\,\,\theta
\vartheta \Rightarrow\,\,\vartheta