Spectre5
- 182
- 0
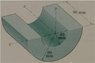
Can someone please help me with this problem...I need to find the mass moment of inertia about the y-axis (see picture)
I know this can be done as two composite areas/volumes and I know that doing this through integration is not the "best" or "easiest" way...but this is how I want to do it...with that said, here is what I have done/tried...but I get the wrong answer...
I_{yy} = mass moment of inertia about the y axis
I_{yy}=\int{\int{\int{(x^2+z^2)}}}dm
I_{yy}=\int{\int{\int{(x^2+z^2)}}}\rho dV
I_{yy}=\rho*\int{\int{\int{(x^2+z^2)}dy}dx}dz
I_{yy}=\rho*\int{\int{\int{(x^2+z^2)}rdr}d\theta}dz
I_{yy}=\rho*\int{\int{\int{((r\cos{\theta})^2+z^2)}rdr}d\theta}dz
I_{yy}=7830*\int_{0}^{.09}{\int_{-\pi}^{0}{\int_{.04}^{.08}{(r^3\cos^2{\theta}+z^2r)}dr}d\theta}dz
I_{yy}=.0355779...
BTW, as you can see, rho is 7830 for this problem
Answer = .0249726... (I found this answer through calculating the mass moment of inertia by composite areas, and I know this is correct)
I know this can be done as two composite areas/volumes and I know that doing this through integration is not the "best" or "easiest" way...but this is how I want to do it...with that said, here is what I have done/tried...but I get the wrong answer...
I_{yy} = mass moment of inertia about the y axis
I_{yy}=\int{\int{\int{(x^2+z^2)}}}dm
I_{yy}=\int{\int{\int{(x^2+z^2)}}}\rho dV
I_{yy}=\rho*\int{\int{\int{(x^2+z^2)}dy}dx}dz
I_{yy}=\rho*\int{\int{\int{(x^2+z^2)}rdr}d\theta}dz
I_{yy}=\rho*\int{\int{\int{((r\cos{\theta})^2+z^2)}rdr}d\theta}dz
I_{yy}=7830*\int_{0}^{.09}{\int_{-\pi}^{0}{\int_{.04}^{.08}{(r^3\cos^2{\theta}+z^2r)}dr}d\theta}dz
I_{yy}=.0355779...
BTW, as you can see, rho is 7830 for this problem
Answer = .0249726... (I found this answer through calculating the mass moment of inertia by composite areas, and I know this is correct)