What is the Mass of Dark Matter in a Spiral Galaxy?

[bowlbase]

Homework Statement

Suppose that a sprial galaxy has the mass profile:

$M_{disk}(r)=M_d[1-(1+\frac{r}{r_{rd}})e^{-\frac{r}{r_{rd}}}]$

Where r_rd=3Kpc. and M_d is unknown.

Like all galaxies, this galaxy also contains dark matter as well as its luminous matter. Using the rotational velocity data, you will separately measure the masses of both components, spiral disk and dark matter halo.

1) Find M_dsuch that the circular velocity predicted by the disk alone would not exceed the observed circular velocity at all radii, even neglecting the contribution from the dark matter?
2) Assume that the total disk mass Md is equal to the maximal value you computed
in part (1). The remaining mass must correspond to the dark matter. At the
Sun's radius of 8 kpc, what is the enclosed mass of dark matter, M_DM(8 kpc), and
how does it compare to the enclosed spiral disk mass at that radius, Mdisk(8 kpc)?

Homework Equations

$v_{circ}=\sqrt{\frac{GM(r)}{r}}$

The Attempt at a Solution

From the data I've been given I find the highest velocity and it's corresponding radius. I plugged this into given equation and plug that into the circular velocity equation. I also converted all of the Kpc to meters and the Km/s to m/s.

so:
$$v_{circ}=\sqrt{\frac{GM_d[1-(1+\frac{r}{r_{rd}})e^{-\frac{r}{r_{rd}}}]}{r}}$$
$$v_{circ}^2=\frac{GM_d[1-(1+\frac{r}{r_{rd}})e^{-\frac{r}{r_{rd}}}]}{r}$$
$$v_{circ}^2\frac{r}{G[1-(1+\frac{r}{r_{rd}})e^{-\frac{r}{r_{rd}}}]}=M_d$$
v=194150m/s
r_rd=3Kpc=9.257(10)¹⁴
r=9Kpc=2.7774(10)¹⁵
1pc=3.086(10)¹¹m

Substituting these values in I get ≈2(10)³⁶kg

The second part, I assume, I just do the same calculations but instead of having M_d in there I'd have (M_d+M_DM). But I think, before I even start that this will be nonsense considering the values I have to put in:

8Kpc=2.4688(10)¹⁵m
v@8Kpc=193979m/s

$$v_{circ}^2\frac{r}{G[1-(1+\frac{r}{r_{rd}})e^{-\frac{r}{r_{rd}}}]}-M_d=M_{DM}$$

M_DM=-9.1(10)³⁴

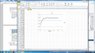
Notice that this is negative. I've attached the data I was given. The left column, I assume, is R and the right is v. It wasn't labeled but I think it is safe to assume such things.

So, what have I done wrong? My galaxy mass seems pretty low considering our own galaxy mass. But I'm not sure where I went wrong. Thanks for any guidance!

 

[mfb]

From the data I've been given I find the highest velocity and it's corresponding radius.

That's not the right datapoint. The disk mass is not allowed to lead to a velocity above the observed one, so you need the datapoint which corresponds to the smallest M_d.

 

[bowlbase]

So, the smallest V of 89 then. I'll work out the calculations again after I make breakfast for my son!

 

[bowlbase]

Okay, everything makes more sense now using that value. Thanks for the help!

 

[bowlbase]

also, i was using the wrong conversion for pc->m. its 10^16 not 10^11