What is the maximum capacitance of the device?

[dect117]

Homework Statement

[/B]
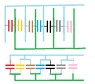
The figure [attached] below shows a variable "air gap" capacitor for manual tuning. Alternate plates are connected together; one group of plates is fixed in position, and the other group is capable of rotation. Consider a capacitor of n = 4 plates of alternating polarity, each plate having area A = 1.60 cm² and separated from adjacent plates by distance d = 4.35 mm. What is the maximum capacitance of the device?

Homework Equations

$$C=\frac {ε_0A} d$$
$$\frac 1 {C_{eq}}=\sum_{j=1}^n \frac 1 {C_j}$$

The Attempt at a Solution

I'm not entirely sure if the capability of the green plates to rotate plays a role here so I just ignored it. I treated each green/blue pair of plates as an individual capacitor.
After that, I plugged in the appropriate values. $$C= \frac {\left( 8.85 \cdot 10^{-12} \right) \left( π \frac {.00016^2} 2 \right)} {4.35 \cdot 10^{-3}}=8.18 \cdot 10^{-17}$$
The capacitors are connected in series, therefore
$$\frac 1 {C_{eq}}=\frac 4 {8.18 \cdot 10^{-17}}$$
$$C_{eq}=\frac {8.18 \cdot 10^{-17}} 4=2.045 \cdot 10^{-17}$$

This is actually a problem from an old assignment so I can't see if it's correct. I have a feeling this is all wrong. Any help would be appreciated!

 

[rude man]

Homework Equations

$$C=\frac {ε_0A} d$$
$$\frac 1 {C_{eq}}=\sum_{j=1}^n \frac 1 {C_j}$$

Bad start! The plates are connected in parallel, not series!

I'm not entirely sure if the capability of the green plates to rotate plays a role here so I just ignored it. I treated each green/blue pair of plates as an individual capacitor.

You get max. capacitance when the plates are closest to each other (fully meshed).

There are 8 plates; how many parallel capacitors does that make?

 

[Merlin3189]

1- Does it not say, "the area of the plates is 1.6 cm²" So why the πr² ?

2- The blue plates are connected, the green plates are connected, so how can the capacitances be in series?

 

[dect117]

Bad start! The plates are connected in parallel, not series!

Is it because the blue plates are touching the second pole? I honestly didn't even notice that the first time I attempted this problem.

You get max. capacitance when the plates are closest to each other (fully meshed).

Right, so I can just treat this problem as if the green plates were fixed in a fully meshed position and ignore the fact that they can move, no?

There are 8 plates; how many parallel capacitors does that make?

Well, a capacitor is comprised of two plates, each carrying an equal amount of opposite charge. So... four, right?

1- Does it not say, "the area of the plates is 1.6 cm²" So why the πr² ?

Darn, I must've rushed when setting up the problem. Simple mistake.

2- The blue plates are connected, the green plates are connected, so how can the capacitances be in series?

I'm not entirely sure yet how they're in parallel, but my guess is that it's because of the second pole. I didn't really notice that at first so I just thought they were connected one after another.

 

[rude man]

Right, so I can just treat this problem as if the green plates were fixed in a fully meshed position and ignore the fact that they can move, no?

Si!

Well, a capacitor comprises two plates, each carrying an equal amount of opposite charge. So... four, right?

This is not necessarily a trivial question. One way to answer it is to compute the total energy stored in the E fields, then equate this to 1/2 CV². Doing it this way the answer is 7. But I wouldn't be surprised if others will debate this derivation & I hope they do.

I'm not entirely sure yet how they're in parallel, but my guess is that it's because of the second pole. I didn't really notice that at first so I just thought they were connected one after another.

Look more carefully at your figure and how the plates are connected, then draw the plate arrangement schematically.

 

[Merlin3189]

I'm not sure what Rudeman is suggesting about the calculation here. Maybe he's allowing for the free-space capacitance of the individual plates or the whole assembly? AFAIK this is nearly always ignored in this sort of calculation. If it were specifically needed, I think you would need to know how the object is placed with respect to surrounding conductors. Even if it were regarded as in free-space, I think it would be a very much more difficult question.

They seem to tell you the area of the plates and the separation of the plates, so you can use your formula directly, provided you know ε₀ for air (I never remember these values and depend on them being given in the question!)
You can see the individual capacitances just by looking at your diagram (Why do people never draw diagrams these days? They're so helpful.)
You can treat it as several separate capacitors, or as one capacitor with several times the area.

 

[rude man]

View attachment 222969
I'm not sure what Rudeman is suggesting about the calculation here. Maybe he's allowing for the free-space capacitance of the individual plates or the whole assembly? AFAIK this is nearly always ignored in this sort of calculation. If it were specifically needed, I think you would need to know how the object is placed with respect to surrounding conductors. Even if it were regarded as in free-space, I think it would be a very much more difficult question.

Not sure I understand. Had nothing to do with surrounding conductors, fringe fielding, or any other non-first-order consideration.

The energy in one of the seven volumes defined by any two adjacent capacitors is
U_i = 1/2 ε₀E² times the volume which is Ad. So the total energy is 7U_i since there are 7 such volumes. We equate this to 1/2 CV² to get C = 7ε₀A/d.

I was happy to see that your answer amounts to the same as mine. And good point about making a drawing.