BurpHa
- 47
- 14
- Homework Statement
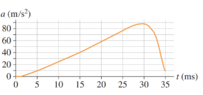
- The jumping ability of the African desert locust was measured by placing the insect on a force plate, a platform that can
accurately measure the force that acts on it. When the locust
jumped straight up, its acceleration was measured to follow the
curve in Figure P4.71. What was the maximum force that this
0.50 g locust exerted on the force plate?
- Relevant Equations
- Newton's Second Law: F = ma.
At the beginning, I just looked for the highest point in the graph, which is approximately 90 \frac m s^2.
Then I plugged it in the formula F = ma and got the force equaled to 0.045 N.
However, when I looked back, the graph is about the change in acceleration. So really, I'm dealing with acceleration of acceleration. From what I understand, the acceleration increases when the locust jumps up until t is approximately about 27 ms, when it starts to decrease.
The answer I get from my book is 0.084 N. When I plug 0.084 N to the formula F = ma, the acceleration is 168 \frac m s^2
I don't understand how it got 168 \frac m s^2 so that it could get 0.084 N.
Thank you for your help.
Then I plugged it in the formula F = ma and got the force equaled to 0.045 N.
However, when I looked back, the graph is about the change in acceleration. So really, I'm dealing with acceleration of acceleration. From what I understand, the acceleration increases when the locust jumps up until t is approximately about 27 ms, when it starts to decrease.
The answer I get from my book is 0.084 N. When I plug 0.084 N to the formula F = ma, the acceleration is 168 \frac m s^2
I don't understand how it got 168 \frac m s^2 so that it could get 0.084 N.
Thank you for your help.
Attachments
Last edited: