What is the minimum refractive index for total internal reflection at point P?

[Neophyte7]

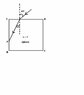
A ray of light strikes a square glass block at an angle of 45 degrees and enters the glass. If this block is surrounded by air (n=1), what is the minimum value of the refractive index of the glass if the total internal reflection occurs at point P. (see attached diagram)

I'm really lost on this one. I know to take Snell's law at the surface AD. And the condition for the total internal reflection at the surface AB.

I know n₁sin(45) = n₂sin(theta) from Snell's law, but how do I get the value for the unknow angle (theta)?

I know that we can determine that the angle at P is sin(90-theta) which = cos (theta)
And I know that sin²(theta) + cos²(theta) = 1. But that's as far as I can get.

Any help would be appreciated. I've attached a diagram for clarification. Thanks.

 

[mgb_phys]

Normally you don't - it's difficult to measure the path of the light inside the glass.
Draw the path of the light ray coming out of the bottom side of the block - then try finding 'n' in terms of the displacement of the ray and the thickness of the block.

 

[Dadface]

The angle of incidence at P=90-theta(the critical angle) and the angle of emergence=90degrees.At P n from air to glass is given by n=sin90/(sin90-theta)=1/cos theta.