alejandrito29
- 148
- 0
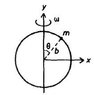
I am reading about the Asimov pendulum (see figure)
The aceleration in spherical coordinates is
##\vec{a} =( R \dot{\theta}^2 - R \omega^2 \sin ^2 \theta) \hat{r} + (R \ddot{\theta} - R \omega ^2 \sin \theta \cos \theta ) \hat{\theta} + (2R \dot{\theta} \omega \cos \theta) \hat{\phi}##
The forze is:
##-mg\hat{y}= -mg\cos(\frac{\pi}{2}-\theta) \hat{\theta} =-mg\sin(\theta) \hat{\theta}##
If i analize the theta component i find the answer for the equation of motion
##R \ddot{\theta} - R \omega ^2 \sin \theta \cos \theta = -g\sin(\theta)##
But, what happen with the other component of equation of motion?, why this does not appear in the books?
##R \dot{\theta}^2 - R \omega^2 \sin ^2 \theta =0##
##2R \dot{\theta} \omega \cos \theta=0##
In the last equation neither of the terms are zero.
Pd: I does not want to use the Lagran
The aceleration in spherical coordinates is
##\vec{a} =( R \dot{\theta}^2 - R \omega^2 \sin ^2 \theta) \hat{r} + (R \ddot{\theta} - R \omega ^2 \sin \theta \cos \theta ) \hat{\theta} + (2R \dot{\theta} \omega \cos \theta) \hat{\phi}##
The forze is:
##-mg\hat{y}= -mg\cos(\frac{\pi}{2}-\theta) \hat{\theta} =-mg\sin(\theta) \hat{\theta}##
If i analize the theta component i find the answer for the equation of motion
##R \ddot{\theta} - R \omega ^2 \sin \theta \cos \theta = -g\sin(\theta)##
But, what happen with the other component of equation of motion?, why this does not appear in the books?
##R \dot{\theta}^2 - R \omega^2 \sin ^2 \theta =0##
##2R \dot{\theta} \omega \cos \theta=0##
In the last equation neither of the terms are zero.
Pd: I does not want to use the Lagran