What is the moment of inertia of an inclined disk?

[Saitama]

Homework Statement

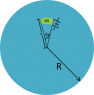
I am trying to find the moment of inertia of a disc (let the mass be m and radius R) inclined at an angle θ to the vertical axis.
(See attachment 1)

Homework Equations

The Attempt at a Solution

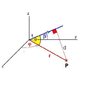
I started by taking a small element of area dA. (see attachment 2)
The mass of this small element is dA*Mass density of disc.
dA=xd$\phi$dx and mass density=m/($\pi$R^2)
Now, moment of inertia is defined as
I=∫dmr^2 (Here r=xsinθ)
$$I=\int_{0}^{2\pi} \int_{0}^{R} \frac{m}{\pi R^2}xd \phi dx(x\sinθ)$$
Solving this, i get
$$I=\frac{4}{3}mRsinθ$$ which i think is completely wrong.

 

[ehild]

Hi Pranav,

It is easier to imagine the problem if you keep that disk horizontal, in the xy plane and the axis in the yz plane is inclined to it with angle β. The distance d of a point P of the disk from the axis is r sin(θ) where θ is the angle the axis and the position vector r enclose: It is not the same as β.

ehild

 

[Saitama]

Hi Pranav,

It is easier to imagine the problem if you keep that disk horizontal, in the xy plane and the axis in the yz plane is inclined to it with angle β. The distance d of a point P of the disk from the axis is r sin(θ) where θ is the angle the axis and the position vector r enclose: It is not the same as β.

ehild

Yes, its now easier to understand the problem.
In my method, i did not realize that θ too varies. But now how am i going to form the integral?

 

[ehild]

At given β, d depends both on φ and r. Find the expression first.

ehild

 

[Saitama]

At given β, d depends both on φ and r. Find the expression first.

ehild

I have tried it for more than half hour but still have no clue, i am unable to express d in terms of φ and r.

 

[ehild]

"d" is the distance of a point from the axis. Can you find the distance of a point from a straight line?

A point on the axis can be written as the vector b=bt where t is the unit vector along the axis. t=cosβj+sinβk.

A point P of the disk is represented by the vector r=rcosφi+rsinφj.

The distance between a point of the axis and P is equal to the magnitude of the difference r-b, and the distance of P from the axis is the shortest distance.
Find the minimum of (r-b)².

ehild

 

[Saitama]

Can you find the distance of a point from a straight line?

Yes.

The distance between a point of the axis and P is equal to the magnitude of the difference r-b, and the distance of P from the axis is the shortest distance.
Find the minimum of (r-b)².

ehild

I get r²(1-cos²φcos²β) as the minimum value of (r-b)². Is this correct?

 

[ehild]

Yes.


I get r²(1-cos²φcos²β) as the minimum value of (r-b)². Is this correct?

I got the same. You can integrate now for the disk

ehild

 

[Saitama]

I got the same. You can integrate now for the disk

ehild

Thanks for the help ehild!
Here's my attempt:
$$dI=\frac{m}{\pi R^2}r(d\varphi)(dr)\cdot r^2(1-\cos^2\varphi \cos^2\beta)$$
Integrating the above expression under the appropriate limits, i get
$$I=\frac{mR^2}{2}\left(1-\frac{cos^2\beta}{2}\right)$$
Is this correct?
Is it valid to use the parallel axis theorem here if i want the MI about an axis parallel to the given axis in the question?

 

[haruspex]

$$I=\frac{mR^2}{2}\left(1-\frac{cos^2\beta}{2}\right)$$

Looks right.

Is it valid to use the parallel axis theorem here if i want the MI about an axis parallel to the given axis in the question?

Sure. Why not?

 

[ehild]

Checking my calculation again, I got d²=r²(1-cos²β sin²φ) with φ the angle with respect to the x axis, as shown in my post #2. But that does not influence the final result.

The parallel axis theorem is valid for any shape and any parallel axes.

ehild