ditzycloud said:
Could anybody explain what "power spectrum" in cosmology means. I am trying to understand the WMAP power spectrum graph, in particular. For example, what do the multiple moments physically represent?
The power spectrum describes how the amplitudes of the primordial perturbations vary with scale. So, for example, a scale-invariant power spectrum is one for which the amplitudes are independent of scale. The primordial perturbations are what gave rise to the large scale structures of today's universe. It's best to start with the correlation function,
<br />
\xi({\bf r}) = \langle \mathcal{R}({\bf x},\tau)\mathcal{R}^\dagger({\bf x}+{\bf r},\tau)\rangle
where x and tau are the space and time coordinates, respectively, and \mathcal{R} is the amplitude of the curvature perturbation. The curvature perturbations are the tiny primordial ripples in spacetime that were the seeds of structure. So the correlation function measures the amount of correlation between an overdensity here with an overdensity there, a distance r away. It is a statistic for describing the clumpiness of the universe as a function of scale. The power spectrum, it turns out, is just the Fourier transform of the correlation function,
<br />
\xi({\bf r}) =\frac{1}{(2\pi)^3}\int \mathcal{P}_\mathcal{R}(k) e^{-i{\bf k}\cdot{\bf r}}d^3k<br />
So, for example, if we had overdensities arranged in a perfectly periodic fashion, the power spectrum would just be a delta function with
k equal to the spacing. But, general overdensities are given in terms of a power spectrum across a range of scales. In fact, what I've defined here, while technically a power spectrum, is not what cosmologists mean when they say "power spectrum." Instead, they mean this:
<br />
P_\mathcal{R}(k) = \frac{d\langle|\mathcal{R}({\bf x},\tau)|^2\rangle}{d{\rm ln}k}<br />
which is really the variance of the curvature perturbation. Nice, I know. But don't let that confuse you. Instead just think of the power spectrum as the amplitude of the perturbation as a function of length scale (or k).
Now, in addition to ultimately giving rise to structure, the first thing the primordial perturbations did was imprint themselves on the CMB, observable today as temperature anisotropies. Now, the CMB today comes to us from all directions, appearing to emanate from a giant sphere with Earth at the center. The inside surface of this sphere -- the so-called
last scattering surface, is what we measure with our satellites. It is this surface that is cut open and spread out to form the spectacular WMAP images like this one:
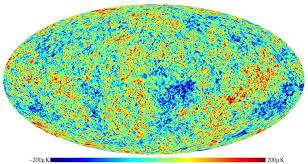
The beautiful curve to which you refer, is a way of representing the degree of clumpiness of this map, much like the correlation function measures the clumpiness of 3D structures in today's universe. But, since the CMB sky is really a spherical surface, we use the angle \theta between points on the sky to parameterize the correlations. And we can likewise take the Fourier transform of this temperature correlation function, just as we did for the 3D correlation function, and we obtain the temperature power spectrum, but this time parameterized in terms of multipole number, \ell, instead of k. Here, small \ell corresponds to large scales (small k). So, for \theta=90 degrees, we are measuring correlations on very large scales, in fact, on scales of order the size of the observable universe. These are the largest scale correlations known, the quadrupole. As we move to smaller angular separations, we observe the octupole, and higher multipoles. Here are the first few multipole moments:
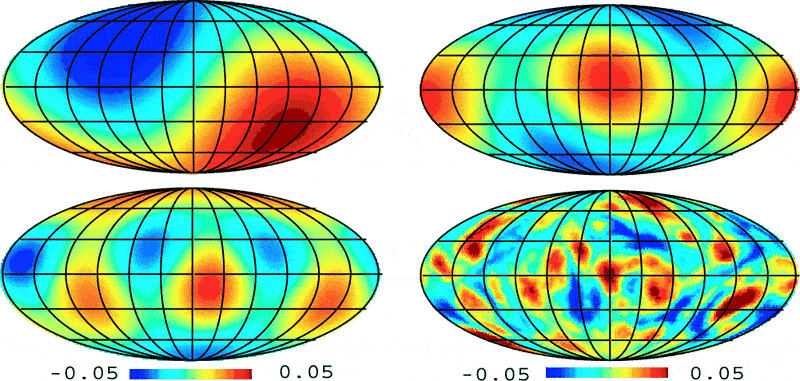
So the CMB sky is really built up out of all of these fluctuations, each multipole moment giving the amplitude of the correlation on a different scale. That's what your curve is showing -- the amplitudes of these fluctuations as a function of angular scale on the CMB sky. It is the Fourier decomposition of the CMB temperature fluctuations on a spherical surface. I've not included the relevant math here for brevity and since I don't want to overly complicate things. In summary, we have a primordial power spectrum, P(k), that describes the scale dependence of the amplitude of the initial perturbations. These give rise to temperature fluctuations in the CMB, which are described by another power spectrum (the C_{\ell}'s). Of course the two power spectra are related: the temperature power spectrum is the primordial perturbation spectrum as an adolescent, after the fluctuations have grown and evolved somewhat, projected onto the sphere.
We can also delve into the different features of this curve, and talk about what this curve teaches us about the history and evolution of the universe. It's a fascinating story, and I'd be happy to discuss more if you're interested.