What is the proof for triangle ABC with known sides and angle relationships?

  • Thread starter Thread starter Blissfulpain
  • Start date Start date
  • Tags Tags
    Proof Triangles
Blissfulpain
ok, I'm in first year coolege and we're doing some review from high school work.. but i can't for the life of me remember how to do one of these questions and i can't seem to get past this one part or at least figure out how to prove that it is what i think it is.

it's going to be a bit trickier, because i can't insert a picture, but i guess that isn't of the most importance anyways. alright

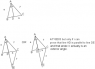
you have triangle ABC.
side AB=4 units
side AC=7 units
the line CD extends for 3 units towards point B, the distance between point B an D is unknown and is what needs to be found
the Angle BCD is = angle DAC

here's what I've tried to do so far...

i've tried to fold the 2 triangles in half across the line AD, which lines up the two sides AB and AC, with the line AC extending 3 units futher then line AB. I'm still trying to follow this train of reasoning.. but so far with little success, i don't really know what to do next, but i think it helps somehow : )

next...

I tried extending the common side between the two triangles, line AD, far enough so that i can draw a new line, 7 units long, from point C, i'll call the intersection point E. The problem arises when i can't prove that the new triangle DEC is the same as triangle ADC. I CAN prove that it is proportional to triangle ABD, but that doesn't help me, because i only know that the side CE is 7 units, the Side DC is 3 units, and i don't know if i can prove that the angle DEC is equal to the angle DAC... which means i can't prove that the line DE is a continuation of the line AD...

hence I'm lost.

thx for the help in advance.. hey, kewl... just found the attacthment thing... i'll go draw a picture and then post :)
 

Attachments

  • Triangle Diagram.png
    Triangle Diagram.png
    5.7 KB · Views: 566
Physics news on Phys.org
Hint: angle bisector theorem.

Hope that helps!
 
nope, doesn't help... i looked it up on the net, and got this "The angle bisector of an angle in a triangle divides the opposite side in the same ratio as the sides adjacent to the angle."

so the angle bisector is line AD, and the adjacent and opposiye side are? i can't assume ANY right angles... and all the other stuff i found on this theorem had something to do with area of a triangle, which i can't do either, because i don't have enough info to find that yet...

a bit more of a hint is needed :confused:
 
Blissfulpain said:
nope, doesn't help... i looked it up on the net, and got this "The angle bisector of an angle in a triangle divides the opposite side in the same ratio as the sides adjacent to the angle."

so the angle bisector is line AD, and the adjacent and opposiye side are? i can't assume ANY right angles... and all the other stuff i found on this theorem had something to do with area of a triangle, which i can't do either, because i don't have enough info to find that yet...

a bit more of a hint is needed :confused:

No right angles required, merely an understanding of the words adjacent and opposite.

Let me paraphrase the theorem for the triangle you've got :

Simply, it says that CD/BD = AC/AB.

Now go back and understand what the theorem is trying to say.
 
so, 3/x=4/7
3/x=1.75
x=1.75*3
x=5.25
huh, i had gotten that number before... just couldn't prove that it was the right number... now i can with that theorem

thx a lot guys :)))))
 
oops... i mean 3/7=x/4
so 3/7=.429
.429x4=1.7 units

therefore BD=1.7
 

Thread '##(A/\mathfrak{a})_{\mathfrak{p}/\mathfrak{a}}## and its isomorphism?'

I asked online questions about Proposition 2.1.1: The answer I got is the following: I have some questions about the answer I got. When the person answering says: ##1.## Is the map ##\mathfrak{q}\mapsto \mathfrak{q} A _\mathfrak{p}## from ##A\setminus \mathfrak{p}\to A_\mathfrak{p}##? But I don't understand what the author meant for the rest of the sentence in mathematical notation: ##2.## In the next statement where the author says: How is ##A\to...
View full post »

Thread 'Questions about non existence of GCDs vs (coimages, cokernels)'

The following are taken from the two sources, 1) from this online page and the book An Introduction to Module Theory by: Ibrahim Assem, Flavio U. Coelho. In the Abelian Categories chapter in the module theory text on page 157, right after presenting IV.2.21 Definition, the authors states "Image and coimage may or may not exist, but if they do, then they are unique up to isomorphism (because so are kernels and cokernels). Also in the reference url page above, the authors present two...
View full post »

Thread 'Decomposition into irreps of compact Lie group'

When decomposing a representation ##\rho## of a finite group ##G## into irreducible representations, we can find the number of times the representation contains a particular irrep ##\rho_0## through the character inner product $$ \langle \chi, \chi_0\rangle = \frac{1}{|G|} \sum_{g\in G} \chi(g) \chi_0(g)^*$$ where ##\chi## and ##\chi_0## are the characters of ##\rho## and ##\rho_0##, respectively. Since all group elements in the same conjugacy class have the same characters, this may be...
View full post »

Similar threads

B A triangle problem: Prove that |AC|+|AB|=|PR|+|PQ| given some constraints
Replies
13
Views
2K
MHB Difference of angles in a triangle
Replies
4
Views
1K
B In a triangle, is the angle between the points of contact of the inscribed circle with the sides 120 degrees?
Replies
2
Views
800
MHB Barycentric coordinates in a triangle - proof
Replies
5
Views
3K
MHB Proving Equality of Angles in an Acute Triangle
Replies
4
Views
1K
MHB Geom Ch: Prove $AB=x^3$ Given $\triangle ABC$ & $\triangle AEF$
Replies
1
Views
1K
MHB What are the angles of an isosceles triangle with a specific ratio?
Replies
2
Views
1K
MHB Acute Triangle ABC: Point P and Line Intersections Formula
Replies
1
Views
2K
I Chiral symmetries in E[SUP]^n[/SUP]
Replies
1
Views
2K
MHB Analytic geometry proof with triangle.
Replies
3
Views
1K

Hot Threads

Recent Insights

Back
Top