Ose90
- 5
- 0
A hemisphere bowl of radius 12cm is initially full of water. Water runs out of a small hole at the bottom of the bowl at a rate of 48pi cm^3 s^-1. When the depth of the water is x cm , show that the depth is decreasing at a rate of 48/[x(24-x)] cm s^-1
Also, find the rate at which the depth is decreasing when
a) The bowl is full.
b)The depth is 6cm.
Another question is in this picture
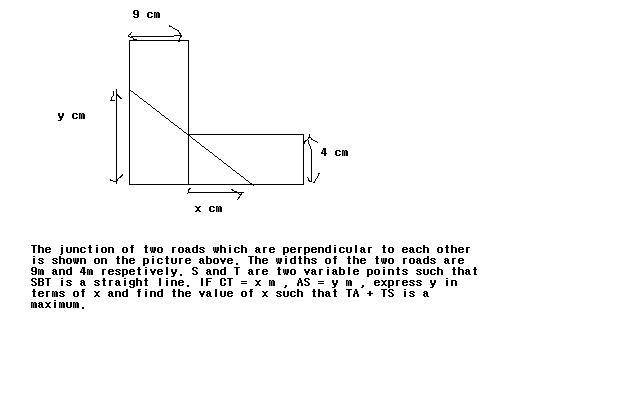
Thanks in advance! Really urgent :)
Also, find the rate at which the depth is decreasing when
a) The bowl is full.
b)The depth is 6cm.
Another question is in this picture
Thanks in advance! Really urgent :)