What is the rate of water decreasing in a hemisphere bowl when the depth is 6cm?

[Ose90]

A hemisphere bowl of radius 12cm is initially full of water. Water runs out of a small hole at the bottom of the bowl at a rate of 48pi cm^3 s^-1. When the depth of the water is x cm , show that the depth is decreasing at a rate of 48/[x(24-x)] cm s^-1
Also, find the rate at which the depth is decreasing when

a) The bowl is full.
b)The depth is 6cm.

Another question is in this picture

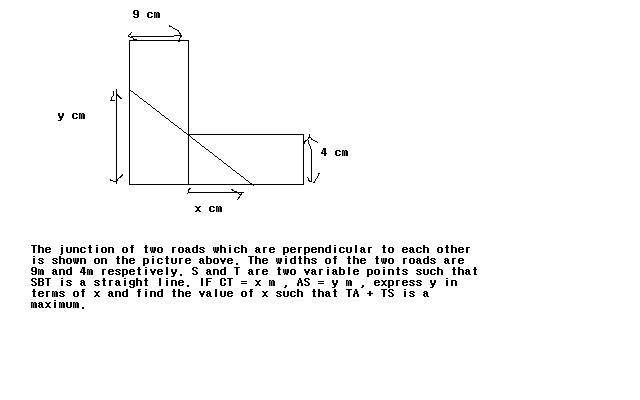
Thanks in advance! Really urgent :)

 

[tiny-tim]

Hi Ose90!

Show us what you've tried, and where you're stuck, and then we'll know how to help.

 

[Ose90]

Hi Ose90!

Show us what you've tried, and where you're stuck, and then we'll know how to help.

Hi tiny-tim, thanks for replying.
Glad to tell you that I have solved it.

However, I will still write down my solution to see if it is correct.

For the first question, I imagine the right side of the semi-circle displaced vertically, I get the equation (x-0)^2 + (y - r)^2 = r^2
then, x^2 = r^2 - (y^2 + r^2 -2yr)
x^2 = r^2 - y^2 -r^2 +2yr
= 2yr - y^2
x = [y(2r - y)]^(1/2)

Hence, when h = x and r = 12 , dV/dx = pi(24x-x^2)

from the question , dv/dt =48 pi

dx/dt = dx/dv x dv/dt
= 48 pi
-----
pi(24x - x^2)

For the second question , I use similar triangle to solve it.

Thanks!