What is the relationship between angular velocity and radius in a pulley system?

[wahaj]

Homework Statement

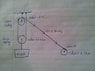
All data is in the attached image. The lower pulley has rotation velocity of 0.6 rad/s but I don't understand why. Both pulleys have same radius and the same rope passes through both of them so why are their velocities different?

Homework Equations

ω = v/r

The Attempt at a Solution

ω = 0.30/0.25 = 1.2 rad/s

 

[haruspex]

Where is the instantaneous axis of rotation of the lower pulley? (That's the point on the pulley which, momentarily, is not moving.)

 

[wahaj]

I don't know what you are talking about. If it has anything to do with the mass then I can't tell you because the mass doesn't have a specific value. It just says mass in the question.

 

[SammyS]

I don't know what you are talking about. If it has anything to do with the mass then I can't tell you because the mass doesn't have a specific value. It just says mass in the question.

The center of mass of the lower pulley is moving. Right? That's quite a different situation than that of the upper pulley, the center of mass of which is stationary.

 

[wahaj]

Right. That's the thing that gets me. The upper pulley is fixed so all it does is rotate. But the lower pulley moves upwards. So the linear velocity of the rope does not only produce angular velocity in the lower pulley but it also produces linear velocity. But I just can't see to grasp the relationship between the two velocities. The only thing I see is that half of the velocity of the rope is used to rotate the pulley and the other half is used to move it upwards. But this is a very specific thing and I highly doubt it will work with other questions

 

[haruspex]

I don't know what you are talking about.

When a wheel rolls along a road, you can think of it as having both rotational and linear speed. That's fine, but it can be useful to understand that at each instant it is actually rotating about its point of contact with the road. This is just another way of looking at it - it gives the same answers.
The lower pulley can be thought of as rolling up a vertical road - the stationary section of string on its right. That means the string on the left is moving up at speed 2rω_lower. It must be moving at the same linear speed over the top pulley, but there it's rω_upper.

 

[wahaj]

I get what you are saying but why in 2rω_lower why 2? why not 3 or 4? I've been trying to think of a reason but I got nothing.

 

[SammyS]

I get what you are saying but why in 2rω_lower why 2? why not 3 or 4? I've been trying to think of a reason but I got nothing.

Again, think of a wheel rolling along a road. The top portion of the wheel is 2r from the road's surface, so the top of the wheel is moving at a speed of 2rω . The center of the wheel moves at rω .

 

[wahaj]

Oh now I get it. I should have thought of this before, I actually did some problems a while back where I had to determine the value of gravitational acceleration acting at different points in a loop on roller coasters. The concept applied here is the same. Thanks I should be able to get the answer now.