What is the role of drag moment in the net momentum formula for quadrotors?

[harmyder]

While watching lecture at Coursera, i tumbled over this fourmula

Moment
$$\mathbf{M}=\sum_{i=1}^{4}(\mathbf{F}_i\times \mathbf{r}_i+\mathbf{M}_i)$$
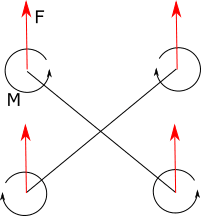
where F is uplift force from a propeller, and M is drag moment for a propeller.

But why they add drag moment(torque) like that? Maybe it will differ for central point.

 

[A.T.]

Maybe it will differ for central point.

Try it out by computing the moments of the blade drag forces around different reference points.

 

[harmyder]

Try it out by computing the moments of the blade drag forces around different reference points.

Thanks, it is true for two points on the picture, but can you name the rule? I want to read it whole to understand it better. Thank you.

 

[harmyder]

Could somebody write what are these $M_i$? Because i still don't understand how it works, i think every moment must be calculated about some point.

I have found this formula
$$\begin{equation}<br /> \dot{\mathbf{H}}_O = \sum(\mathbf{r}_i \times m_i\dot{\mathbf{v}}_i) = \sum(\mathbf{r}_i \times \mathbf{F}_i + \mathbf{M}_i)<br /> \end{equation}$$
but i don't understand from where $\mathbf{M}_i$ came, because i think that $m_i\dot{\mathbf{v}}_i = \mathbf{F}_i$

 

[A.T.]

i don't understand from where $\mathbf{M}_i$ came,

Didn't you explain it yourself:

and M is drag moment for a propeller.

It's the total moment of all aerodynamic forces on the blades, which are in the plane of the propeller disc.

 

[harmyder]

Didn't you explain it yourself:

Well, yes, but here i want to know from where $M$ came in this general formula $(1).$ It is unrelated for quadrotor, just to understand underlying theory.

 

[A.T.]

Well, yes, but here i want to know from where $M$ came in this general formula $(1).$ It is unrelated for quadrotor, just to understand underlying theory.

In general it's just some external moment.