What is the significance of neglecting the encircled sides in Ampere's law?

[JD_PM]

Homework Statement

Magnetic field over a plane

Relevant Equations

$\int B dl = 0$

This is a very basic issue but really important as well.

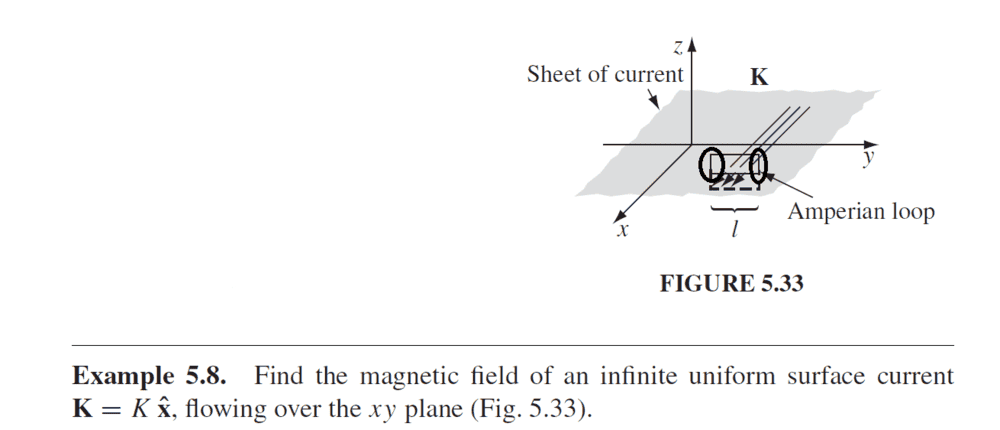
The rectangular loop has length $l$ and width $h$. I have seen the argument of neglecting the encircled sides of the loop because $h << 1$ while using Ampere's law to calculate the magnetic field flowing over a plane.

I find this argument not convincing enough. What I think it happens is that an infinitesimal segment of $h$, which is $dl$, is perpendicular to $B$ (one can see that using the right hand rule). And thus on both encircled sides:

$$\int B dl = 0$$

Am I correct?

Thanks.

 

[BvU]

https://en.wikipedia.org/wiki/Current_sheet#Magnetic_field_of_an_infinite_current_sheet

 

[JD_PM]

https://en.wikipedia.org/wiki/Current_sheet#Magnetic_field_of_an_infinite_current_sheet

Thanks. Now I see that

What I think it happens is that an infinitesimal segment of $h$, which is $dl$, is perpendicular to $B$ (one can see that using the right hand rule). And thus on both encircled sides:

$$\int B dl = 0$$

Is correct.

 

[BvU]

Better keep to the vector notation, though...

 

[JD_PM]

$$\oint \vec B \cdot \vec {dl} = 0$$