Benjamin_harsh
- 211
- 5
- Homework Statement
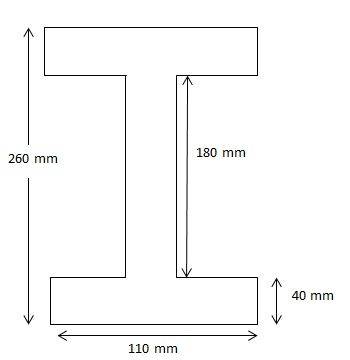
- What is the area moment of inertia for this problem?
- Relevant Equations
- ##I_{2} = I_{3} = \large\frac{1}{12}\normalsize bh^{3} = \large \frac{1}{12}\normalsize *35*(180 mm)^{4} = 1.701*10^{7} mm^{4}##
##I_{total} = (I_{1} + A_{1}d_{1}^{2} ) + (I_{2} + A_{2}d_{2}^{2}) + (I_{3} + A_{3}d_{3}^{2})##(d is the distance between centroid of the individual box and centroid of whole shape.)
By negative area method by joining the gaps in I section.
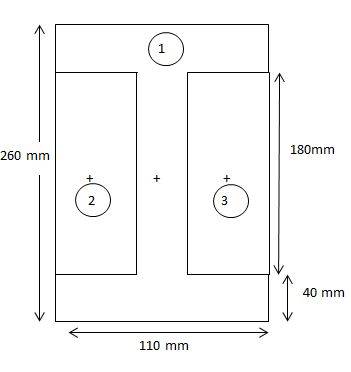
##I_{total} = (I_{1} + A_{1}d_{1}^{2} ) - (I_{2} + A_{2}d_{2}^{2}) -(I_{3} + A_{3}d_{3}^{2})##
Centroid of two new sections matches with centroid of final shape. So ##d_{1}##, ##d_{2}## and ##d_{3}## are zero.
##I_{total} = (I_{1} - I_{2} - I_{3})##
Moment of Inertia of a Rectangle 1,##I_{1} = \large \frac {1}{12}\normalsize bh^{3} = \large \frac {1}{12}\normalsize 110*260^{3}
= 1.611 * 10^{8}mm^{4}##
Moment of Inertia of a Rectangle 2 and 3 are equal because they have similar dimensions ##I_{2} = I_{3} = \large\frac{1}{12}\normalsize bh^{3} = \large \frac{1}{12}\normalsize *35*(180 mm)^{4} = 1.701*10^{7} mm^{4}##
Area moment of Interia, ##I_{total} = I_{1} - 2I_{2} = 1.272*10^{8} mm^{4}##
By negative area method by joining the gaps in I section.
##I_{total} = (I_{1} + A_{1}d_{1}^{2} ) - (I_{2} + A_{2}d_{2}^{2}) -(I_{3} + A_{3}d_{3}^{2})##
Centroid of two new sections matches with centroid of final shape. So ##d_{1}##, ##d_{2}## and ##d_{3}## are zero.
##I_{total} = (I_{1} - I_{2} - I_{3})##
Moment of Inertia of a Rectangle 1,##I_{1} = \large \frac {1}{12}\normalsize bh^{3} = \large \frac {1}{12}\normalsize 110*260^{3}
= 1.611 * 10^{8}mm^{4}##
Moment of Inertia of a Rectangle 2 and 3 are equal because they have similar dimensions ##I_{2} = I_{3} = \large\frac{1}{12}\normalsize bh^{3} = \large \frac{1}{12}\normalsize *35*(180 mm)^{4} = 1.701*10^{7} mm^{4}##
Area moment of Interia, ##I_{total} = I_{1} - 2I_{2} = 1.272*10^{8} mm^{4}##
Last edited: