What is the true definition and meaning of sin/cos/tan?

[physior]

hello

we define sin/cos/tan as the ratio of sides of a right triangle, which we have proved (? not sure, or we assume by a theorem or something?) that are constant for a specific angle

this makes some sense

but what about sin/cos/tan for degrees like 0, 90, >90 ? what about negative degrees? what about degrees >360? (as the sin function goes to negative numbers and numbers above 360 degrees)

it clearly seems that sin/cos/tan is not just the ratio of a right angle sides, but something else

why they use that definition and they confuse us?

what is the real sin/cos/tan definition and what its real meaning?

thanks

 

[Fredrik]

This definition defines sin t and cos t for arbitrary real numbers t:

The circle is the unit circle, i.e. the circle of radius 1, defined by $x^2+y^2=1$.

One way of stating this definition in words is that to say that cos t is the new x coordinate of the point (1,0) after a clockwise rotation by an angle t, and sin t is the new y coordinate of the point (1,0) after the same rotation.

There's an even more general definition that works for complex values of t as well:

\begin{align}
\sin x & = x - \frac{x^3}{3!} + \frac{x^5}{5!} - \frac{x^7}{7!} + \cdots \\
& = \sum_{n=0}^\infty \frac{(-1)^n x^{2n+1}}{(2n+1)!}, \\
\cos x & = 1 - \frac{x^2}{2!} + \frac{x^4}{4!} - \frac{x^6}{6!} + \cdots \\
& = \sum_{n=0}^\infty \frac{(-1)^n x^{2n}}{(2n)!}.
\end{align}
(I just copied this formula from Wikipedia. That's why it says x instead of t).

 

[physior]

is there a reason why we use sin/cos/tan as defined by the unit circle? is there a practical meaning? for example in natural phenomena, is there a reason to calculate the values of x and y by the method of unit circle?

 

[Fredrik]

I'm more interested in foundational issues than applications, so I usually find it very difficult to come up with examples, but I can think of one good example here: The harmonic oscillator. This is just a mass m moving under the influence of a force F=-kx where k is a positive real number. This is approximately what the force will be in the situation shown in the pictures on the right here.

At all times t, we have $mx''(t)=F=-kx(t)$. If we define $\omega=\sqrt{\frac k m}$, we can rewrite this differential equation as $x''(t)+\omega^2x(t)=0$. Note that this holds for all t. The functions f and g defined by $f(t)=\sin\omega t$ and $g(t)=\cos\omega t$, where sin and cos are defined for all real numbers (i.e. defined using the unit circle), are easily seen to be solutions to this differential equation.

As you can see, the input to the function isn't always an angle. In this case it's time.

 

[physior]

can't you just explain with words, not maths? I don't know differentiation

 

[Fredrik]

You should understand the result even if you don't know how to verify it, so I'm not sure what I can explain. The verification can't be done without math. The block in the picture I linked to in post #4 will move (approximately) as the blue ball in this annoying image (but horizontally instead of vertically).

For all real numbers t, the position at time t is given by $\sin\omega t$, where $\omega$ is a positive real number. Since t is any real number here, the triangle definition is clearly inadequate.

 

[SteamKing]

is there a reason why we use sin/cos/tan as defined by the unit circle? is there a practical meaning? for example in natural phenomena, is there a reason to calculate the values of x and y by the method of unit circle?

The unit circle method is one way of defining sin, cos, and tan. Another way is shown in the image below:

If we make the hypotenuse of the triangle, c = radius of the circle = 1, then the defined values of sin and cos become the coordinates of the points on the circle, or cos A = b/c = x, and sin A = a/c = y, with tan A = sin A / cos A = a / b = x / y.

 

[Fredrik]

The unit circle method is one way of defining sin, cos, and tan. Another way is shown in the image below:

True, but the OP asked specifically about sin t for values of t such that this definition doesn't make sense.

 

[vela]

Why do they use that definition and confuse us?

Probably because in the most common applications of trig, you apply it to situation involving a right triangle with an acute angle. A typical example would be when you resolve a force into horizontal and vertical components.

what is the real sin/cos/tan definition and what its real meaning?

There is no "real" definition. You get to choose whatever definition you'd like as long as it works. Typically you choose the one which to be most convenient for whatever you're trying to do unless you're a masochist.

 

[SteamKing]

True, but the OP asked specifically about sin t for values of t such that this definition doesn't make sense.

But he also asked why the unit circle was used to define sin, cos, and tan.

By relating the traditional definitions of sin, cos, and tan to the first quadrant of the unit circle, then you can generalize the calculation of the sin, cos, and tan to the other three quadrants, and finally, you can also see that the function values are periodic after going completely around the circle.

Throwing in harmonic motion and infinite series just made the OP more confused, IMO.

 

[Fredrik]

But he also asked why the unit circle was used to define sin, cos, and tan.

Yes, after saying that he's familiar with the triangle definition and asking for more general definitions that work for larger angles and negative angles, he got the unit circle definition, and asked a follow-up question about it.

Throwing in harmonic motion and infinite series just made the OP more confused, IMO.

He specifically asked for natural phenomena in the follow-up question.

 

[HallsofIvy]

The difficulty with the "right triangle" definition of the trig functions is that the angle must be between 0 and 90 degrees (0 and \pi/2 radians). In order to have the trig functions defined for all real numbers we need some other definition for sine and cosine. The "circle definition" is commonly used. That also has the advantage of making it obvious that the trig functions are periodic, perhaps their most important property.

It is also perfectly valid to define the sine and cosine as power series:
To define sin(x) as \sum_{n=0}^\infty\frac{1}{(2n+1)!}x^{2n+1} and
define cos(x) as \sum_{n=0}^\infty \frac{1}{(2n)!)}x^{2n}

As well as defining y= sin(x) to be the unique function satisfying the differential equation \frac{d^2y}{dx^2}= -y with the initial condition y(0)= 0, y'(0)= 1; and defining y= cos(x) to be the unique function satisfying the differential equation \frac{d^2y}{dx^2}= -y with the initial condition y(0)= 1, y'(0)= 0.

 

[BiGyElLoWhAt]

The only reason your triangle has to be acute in order to use the triangle definition is because it also has to be a right triangle. You can't have an obtuse right triangle.

 

[Mark44]

Inasmuch as the OP has posted his question in the Precalc section, explanations involving differential equations or Maclaurin series are not helpful to his understanding.

 

[BiGyElLoWhAt]

Inasmuch as the OP has posted his question in the Precalc section, explanations involving differential equations or Maclaurin series are not helpful to his understanding.

LoL

 

[olivermsun]

We use the unit circle because the sine, cosine, tangent are all various ratios of sides of a right triangle (see SteamKing's post #7). Since they are ratios, you can always scale the triangle to one with the same ratios (a similar triangle) but with 1 as the length of the hypotenuse. Then you can fit the triangle in the unit circle, as shown in Fredrik's post (#2).

 

[BiGyElLoWhAt]

Alright, I know this is an older post, but I'll rectify the dead.

The way I look at things is like so:
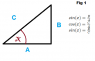
We define sin(theta) as the ratio of the opposite side of the angle theta on a right triangle to the hypotenuse.
We define cos(theta) as the ratio of the adjacent side of the angle theta on a right triangle to the hypotenuse.
We define tan(theta) as the ratio of the opposite side of the angle theta on a right triangle to the adjacent.

What other people are talking about all stems from these definitions. We can express sin(x) as a power series and assign a numerical value to it, which is very useful.

We can also plot sin/cos values on a graph all the way from 0 to 2 pi (360 degrees). This also proves to be a very useful for modeling how sin and cos have a sort of give and take relationship.

If you look at figure 1 (attached), you can see the definition for sine, cosine, and tangent in terms of a right triangle.
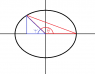
Now if you take those equations and apply them to the triangles in figure 2, you can see how they work together.

Take an arbitrary triangle, and remember, this is a (semi) circle, so all the hypotenuses are the same, and they're equal to the radius of the circle. This gives (for each point "made by a triangle") that x = r*cos(theta), y = r*sin(theta) so the point in question is $(r*cos(\theta),r*sin(\theta))$

There's also a special case for this circle, it's called the unit circle, where the radius (and in turn the hypotenuse of any triangle drawn within the circle) has a length of 1 unit. For this circle, any point on the circle is represented by the coordinates $(x,y) = (cos(\theta),sin(\theta))$

This is pretty useful in many applications. Now while you can't necessarily visualize (define?) these trig functions for obtuse angles, if you look at the points on a circle, you can see what's going on a little better. Standard protocal for measuring an angle is to start from the positive x-axis and measure around to the positive y-axis and continuing around the circle through negative x, negative y, and then back to positive x. Let the angle be larger than pi/2 (90 deg) and you have an obtuse angle. If we look at a unit circle, we can see that the point in question is $(x,y) = (cos(\theta),(sin(\theta))$
Let's look at a unit circle with an obtuse angle representing our triangle in question. If we do so, we can see that cosine has the same value as the x component of the point on the circle for that given angle. Well we can't really do much with an obtuse triangle, but we can use our obtuse triangle to create a right triangle. See figure 3. If we call the angle of the new (right) triangle $\Phi = \pi - \theta$ (180deg - theta) we can easily determine the magnitude of the x value of that point. Looking at the diagram, we can see that the point lies in quadrant 2, meaning all x values are negative, giving us the sign for our point (and in turn our cos value) ! We can repeat this process for the y component and sin value.

I wrote this post in pieces, so I hope it all makes sense.

 

[piethein21]

I think the unit circle is taken not because of physical reasons but mathematical ones.
The main reason I think is because of the
$e^{i\theta}=\cos{\theta}+i\sin{\theta}$ (how do i add latex in my reply...I am new).
Suppose it had radius 2 then we would have
$2=e^{i2\pi}=e^{i\pi}e^{i\pi}=-2*-2$
which does not seem right

 

[Matterwave]

I think the unit circle is taken not because of physical reasons but mathematical ones.
The main reason I think is because of the
$e^{i\theta}=\cos{\theta}+i\sin{\theta}$ (how do i add latex in my reply...I am new).
Suppose it had radius 2 then we would have
$2=e^{i\2pi}=e^{i\pi}e^{i\pi}=-2*-2$
which does not seem right

Use double $'s instead of single $, and use double #'s for in-line latex.

 

[piethein21]

thank you :)

 

[olivermsun]

I think the unit circle is taken not because of physical reasons but mathematical ones.
The main reason I think is because of the
$e^{i\theta}=\cos{\theta}+i\sin{\theta}$ (how do i add latex in my reply...I am new).
Suppose it had radius 2 then we would have
$2=e^{i2\pi}=e^{i\pi}e^{i\pi}=-2*-2$
which does not seem right

$\cos{\theta}$ and $\sin{\theta}$ are ratios, so they have the same values whether you inscribe the triangle in a circle of radius 2 or in the unit circle.

 

[piethein21]

you could see them as ratios yes and you can use them to calculate lengths of triangles and then indeed the radius does not matter but
the equation I gave is an equation which is very helpful and would be lost if you take another radius (as shown in the example).

 

[olivermsun]

Where does the radius appear in your equation?

 

[piethein21]

in the cos(pi)=-2 if the radius is 2
(also see http://en.wikipedia.org/wiki/Euler's_identity)

 

[olivermsun]

Please explain how you use Euler's identity to get that result.

Also, is there a specific equation or figure on the Wikipedia page that I should be looking at?

 

[piethein21]

if you take radius 1:
$e^{i2\pi} = cos(2\pi)+i sin(2\pi)=1+ 0i$ since you "walked" an entire circle (just filling in the Eulers identity).
walking an entire circle is the same as walking 2 half circles mathematically :
$e^{i2\pi}=e^{i\pi}e^{i\pi}$
walking half a circle gives
$e^{i\pi}=cos(\pi)+i sin(\pi)=-1+0i$

so we get 1= -1 *-1 which is true

if you do the same with radius 2 you get 2=-2*-2 which is wrong.

so if you would do radius 2 the Euler identity does not hold anymore

 

[olivermsun]

I understand Euler's identity. What I am hoping you will clarify is how any of that changes when the circle is radius 2.

 

[Fredrik]

I understand Euler's identity. What I am hoping you will clarify is how any of that changes when the circle is radius 2.

He's not saying that it does. He's saying that if we apply some standard formulas for a circle of radius 1 to a circle of radius 2, we get nonsense, as expected.

The fact that $|e^{i\theta}|=1$ for all real numbers $\theta$ implies that Euler's identity can't still hold if we redefine $\sin$ and $\cos$ as coordinates of points on a circle of radius 2.

 

[piethein21]

because $cos(\pi)$ will be -2 then instead of -1

 

[olivermsun]

He's saying that if we apply some standard formulas for a circle of radius 1 to a circle of radius 2, we get nonsense, as expected.

The fact that $|e^{i\theta}|=1$ for all real numbers $\theta$ implies that Euler's identity can't still hold if we redefine $\sin$ and $\cos$ as coordinates of points on a circle of radius 2.

Hmm. Well, the $x$ and $y$ coordinates are exactly the opposite/hypotenuse and adjacent/hypotenuse ratios ($\sin$ and $\cos$) on the unit circle, where the hypotenuse has length 1, and this relationship does not hold on a circle of any other radius.

So I guess I am sort of not getting the OP's point (or maybe that was the OP's point).

 

[Mark44]

I think the unit circle is taken not because of physical reasons but mathematical ones.
The main reason I think is because of the
$e^{i\theta}=\cos{\theta}+i\sin{\theta}$ (how do i add latex in my reply...I am new).
Suppose it had radius 2 then we would have
$2=e^{i2\pi}=e^{i\pi}e^{i\pi}=-2*-2$
which does not seem right

Correct - it's not right. $e^{i 2\pi} = cos(2\pi) + i sin(2\pi) = 1 + 0i = 1$
You can't just come along and set this expression to 2.

 

[BiGyElLoWhAt]

I think the unit circle is taken not because of physical reasons but mathematical ones.
The main reason I think is because of the
$e^{i\theta}=\cos{\theta}+i\sin{\theta}$ (how do i add latex in my reply...I am new).
Suppose it had radius 2 then we would have
$2=e^{i2\pi}=e^{i\pi}e^{i\pi}=-2*-2$
which does not seem right

You're not using euler formula correctly.
$e^{i\theta}=\cos{\theta}+i\sin{\theta}$
This is correct.

but this:
$2=e^{i2\pi}=e^{i\pi}e^{i\pi}=-2*-2$
is not.

$2 = e^{i*2\pi} + e^{-i*2\pi} = 2e^{i*2\pi} = cos(2\pi) + i*sin(2\pi) + cos(2\pi) - i*sin(2\pi)$
OR $=2[cos(2\pi) + i*sin(2\pi)$
the first expansion is a representation of the first eulers, and the second expansion is a representation of the second eulers.

You have $e^{i\theta} = \cos{\theta}+i\sin{\theta}$
and $e^{i*k\theta}= \cos{k\theta}+i\sin{k\theta}$
Where k can be any function.

 

[Fredrik]

You're not using euler formula correctly.
$e^{i\theta}=\cos{\theta}+i\sin{\theta}$
This is correct.

Actually, using the alternative definitions of sin and cos that piethein21 was considering there, it's not. His sin and cos are exactly 2 times the normal sin and cos. So the left-hand side and the right-hand side don't have the same absolute value, unless we also redefine the exponential function as 2 times the normal exponential function. Of course, if we do that, then $e^{x+y}=e^xe^y$ doesn't hold, so his calculation is still wrong.

but this:
$2=e^{i2\pi}=e^{i\pi}e^{i\pi}=-2*-2$
is not.

It's probably time to close this thread, since it has drifted off topic. The OP just wanted to know how to define sin and cos with a domain larger than $[0,2\pi]$. That was answered early in the thread. Most of the posts after that are based on misunderstandings and have nothing to do with the original topic.

 

[piethein21]

the time it was not properly used was to show it did not hold when rules where altered (so I am very aware that it was not correct). I agree with fredrik let's close the thread ... it is drifting...