randomgamernerd said:
can you explain with a diagram[emoji28]
Try to draw your own diagram from this description:
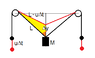
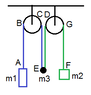
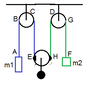
Suppose a section of string is passing up and over a pulley at speed u.
That means every part of the string section must be getting closer to the pulley at that rate.
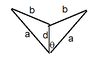
If we take some point on this string we can resolve its velocity into two components: one along the string and one normal to it.
E.g. with u=0 it could still happen that the string is revolving around the pulley for some reason.
We can call these components the radial and tangential velocities.
At any instant, the tangential velocity varies along the string, being maximum where it contacts the mass. Let the tangential speed there be v and the angle the string makes to the vertical be θ.
We know that the end of the string contacting the mass moves vertically, so the horizontal components of the tangential and radial velocities cancel there:
u sin(θ) = v cos(θ)
In the context of the question, both the radial velocity, u, and the tangential velocity contribute to the rising speed of the mass.
The contribution from u is u cos(θ) and from the tangential speed v sin(θ) = u sin(θ)tan(θ). So the upward speed of the mass must be
u cos(θ)+u sin(θ)tan(θ) = u(cos
2(θ)+sin
2(θ))/cos(θ) = u sec(θ).
Alternatively, we could have got there much faster by looking at it the other way around. If the mass is getting nearer to the pulley at rate u then the component of its motion that is towards the pulley must be u: u = w cos(θ).
But I went through the other analysis to show why your method went wrong: you left out the tangential motion of the string.