stealthezio
- 10
- 0
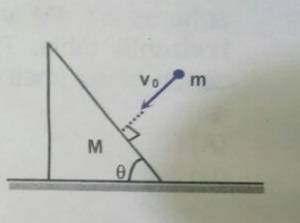
1. In the figure shown , a ball of mass m collides perpendicularly on a smooth stationary wedge of mass M , kept on a smooth horizontal plane. If the coefficient of restitution is e , then determine the velocity of the wedge after collision.
 https://postimage.org/][/PLAIN]
https://postimage.org/][/PLAIN]
Given
mass of ball = m
mass of wedge = M
coefficient of restitution = e
velocity of wedge after collision = ?
answer to problem =
(1+e)mv sinθ / M+m sin^2 θ2.
mv = mv1 + Mv2
v1 = velocity of m after collision
v2 = velocity of M after collision
e = relative velocity after collision / relative velocity before collision
So I tried conservation of momentum along the common normal , ie at the line of impact but since the wedge can only move in x direction I am stumped and cannot get an answer after solving. Tried center of mass approach and still arriving at weird solution. Any advice will be appreciated. Thanks.[/B]
Given
mass of ball = m
mass of wedge = M
coefficient of restitution = e
velocity of wedge after collision = ?
answer to problem =
(1+e)mv sinθ / M+m sin^2 θ2.
mv = mv1 + Mv2
v1 = velocity of m after collision
v2 = velocity of M after collision
e = relative velocity after collision / relative velocity before collision
The Attempt at a Solution
So I tried conservation of momentum along the common normal , ie at the line of impact but since the wedge can only move in x direction I am stumped and cannot get an answer after solving. Tried center of mass approach and still arriving at weird solution. Any advice will be appreciated. Thanks.[/B]
Last edited by a moderator: