Longstreet
- 98
- 1
So, the thermal radiation power off a surface is P=\sigma AT^4.
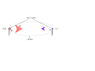
Here I have two cylinders of equal height but different radius. They are stacked on top of each other inside of two cones stacked on top of each other. The idea is that the thermal radiation off of one cyclinder is reflected into the other one.
With this information I know the power off the two cylinders is:
P_1 = \sigma(2{\pi}r_1h/2)T_1^4
and
P_2 = \sigma(2{\pi}r_2h/2)T_2^4
Where P is the power, h is the height of the stack, r is the radius of each cylinder, and T is their temperature.
So say I want P_2<P_1. All I need to do is make r_2 small enough. Solving I get the simple relation r_2<\frac{T_1^4}{T_2^4}r_1.
I know this is extreamly idealized, but what is causing P_2 \geq P_1.
Here I have two cylinders of equal height but different radius. They are stacked on top of each other inside of two cones stacked on top of each other. The idea is that the thermal radiation off of one cyclinder is reflected into the other one.
With this information I know the power off the two cylinders is:
P_1 = \sigma(2{\pi}r_1h/2)T_1^4
and
P_2 = \sigma(2{\pi}r_2h/2)T_2^4
Where P is the power, h is the height of the stack, r is the radius of each cylinder, and T is their temperature.
So say I want P_2<P_1. All I need to do is make r_2 small enough. Solving I get the simple relation r_2<\frac{T_1^4}{T_2^4}r_1.
I know this is extreamly idealized, but what is causing P_2 \geq P_1.
Attachments
Last edited: