mic* said:
When considering the curiosity of why an aerofoil makes lift, angle of attack should not enter the discussion because it is clear that a non-aerofoil shape will "lift" in the direction of the leading edge as it passes through the air. A child sticking their hand out a car window realizes this (not that they should do this).
Bernoulli's principle helps descirbe the way an aerfoil (at 0deg aoa) can make lift, but this is not the wholle story, esp. once considering factors like dihedral, sweep, and even surface finish.
Angle of attack is absolutely critical in determining lift for any shape. In fact, angle of attack is the single most important factor in determining the lift on a shape and has a much greater effect on the lift than do things like thickness or camber. This is doubly true for a supersonic airfoil, where angle of attack is literally the only factor in the lift for a given shape.
Also, the only effect surface finish has on lift is that it has an effect on the laminar-turbulent transition of the wing boundary layer, which can change the effective shape of the wing since turbulent boundary layers are thicker. This is a relatively small effect in most cases, though.
rcgldr said:
Not quite all, since the energy of the air is increased when a wing passes through, Bernoulli is violated somewhat since the Bernoulli principle assumes that total energy remains constant. This issue is more clearly demonstrated in the case of a propeller, where the increase in energy is significant. From this NASA article on propellers:
I am sorry but you don't know what you are talking about here. If you have a wing moving through a fluid or with fluid moving over it, if you have a complete picture of the velocity profile, you can calculate lift from Bernoulli's principle to very high accuracy. Not only
can you do it, but it is done all the time.
You can't "somewhat" violate Bernoulli's principle. Either the conditions for its use hold (classically inviscid, steady, and incompressible, with few exceptions) or they don't. For the example of the wing, moving through the air at a constant rate, you are basically already maintaining any force or energy balance by assuming the constant rate. In particular, you assume that any thrust generated by a propeller or another engine is exactly countering the drag according to Newton's laws. So then, you have to look at the flow field and look at exactly where the conditions for Bernoulli's equation hold (if they do).
So, for an airfoil moving less than Mach 0.3, the flow is incompressible, so let's stick to that regime. We are already talking about a steady flow, so the remaining question is whether the flow is inviscid or not. You can assume the flow is inviscid and calculate the velocities fairly accurately using a panel method or an Euler code that simply enforces the Kutta condition on the trailing edge (which simulates viscosity without actually acknowledging it exists). In that case, Bernoulli's equation is valid and you can get a good estimate of the drag on a wing from a purely inviscid analysis assuming the wing is not stalled.
Now, you may be saying, "but boneh3ad, air is inherently viscous so that example is not really physically true." True though that may be, as it turns out, you can also handle this easily here. One approach is that you make corrections to the shape of the airfoil in your inviscid analysis to account for the presence of the boundary layer (via displacement thickness) and get a much more accurate estimate of the flow field. In that case your analysis is still inviscid and the flow can still be analyzed with Bernoulli's equation.
The other approach is to actually take viscosity into account and solve the full flow equations (or let nature do it for you). Using one of the many neat properties of fluid flows, you can still get the lift for this situation using Bernoulli's equation despite the fact that the analysis is now viscous in nature. As it turns out, when a viscous fluid flows over a surface, it forms a boundary layer whereby the velocity smoothly goes from zero at the wall to the free stream value. However, this effect is confined to the region very close to the surface, and outside of the boundary layer, the flow behaves exactly like an inviscid flow. It also turns out that nature was kind to us in that the pressure gradient in the wall-normal direction in the boundary layer is effectively zero, meaning the static pressure at the surface is the same as it is in the free stream at the edge of the boundary layer at that point. In other words, you can get your "exact" flow field from a viscous analysis of a wing and simply apply Bernoulli's equation only to the inviscid region of the flow and still come up with the correct lift.
In the inviscid region, the total energy
does remain constant, and any energy loss taking place in the viscous region through dissipation is exactly counteracted by assuming a steady flow (and in the real world by the propeller or jet engine). In other words, the conditions for the use of Bernoulli's equation hold. This is also why the same principle does not work for a propeller, since they are, by design, supposed to be dumping much more energy into the flow than the dissipative forces on the propeller itself would require to break even.
Of course, it is still important to understand that Bernoulli's equation in no way explains why the flow moves faster over the upper surface. It is merely a tool that can be used to calculate the lift from a flow field known a priori.
 I'm wondering what makes the air move faster above the wing. I have some questions about this:
I'm wondering what makes the air move faster above the wing. I have some questions about this: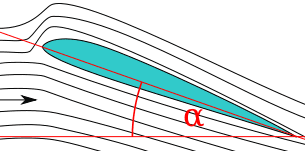 ), wouldn't that also create more air resistance on top of the wing and thereby less speed? Why doesn't it?
), wouldn't that also create more air resistance on top of the wing and thereby less speed? Why doesn't it?