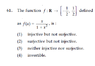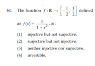You are using an out of date browser. It may not display this or other websites correctly.
You should upgrade or use an alternative browser.
You should upgrade or use an alternative browser.
AI Thread Summary
The discussion revolves around determining the nature of a function's injectiveness and surjectiveness based on its domain and range. Participants agree that the function is injective, as each value in the domain corresponds to a unique value in the range, but there is debate about its surjectiveness since not all potential range values are utilized. The domain is specified as -0.5 to +0.5, with the resulting range being -0.4 to +0.5, leading to confusion about whether the function is surjective. Suggestions include using the intermediate value theorem to analyze the function's behavior and confirming whether it is continuous. Overall, the conversation emphasizes the importance of understanding function properties in mathematical analysis.
Physics news on Phys.org
.Scott
Science Advisor
Homework Helper
- 3,796
- 1,853
Member advised against giving too much help
I believe it is injective but not surjective.
The domain is defined as -0.5 to +0.5.
The resulting range is -0.4 to +0.4.
So every value in the domain yields a unique value in the range (injective).
But there are some values in the potential range (-0.5 to -0.4 and 0.4 to 0.5) which are not used.
The domain is defined as -0.5 to +0.5.
The resulting range is -0.4 to +0.4.
So every value in the domain yields a unique value in the range (injective).
But there are some values in the potential range (-0.5 to -0.4 and 0.4 to 0.5) which are not used.
Last edited:
DrClaude
Mentor
- 8,477
- 5,693
Really?.Scott said:The domain is defined as -0.5 to +0.5.
The resulting range is -0.4 to +0.5.
@alijan kk: What are the domain and the range of the function? What is the meaning of injective and surjective?
Dick
Science Advisor
Homework Helper
- 26,254
- 623
.Scott said:I believe it is injective but not surjective.
The domain is defined as -0.5 to +0.5.
The resulting range is -0.4 to +0.5.
So every value in the domain yields a unique value in the range (injective).
But there are some values in the potential range (-0.5 to -0.4 and 0.4 to 0.5) which are not used.
Aside from the fact that is wrong, I would like to hear what alijan kk thinks the range is, and why.
.Scott
Science Advisor
Homework Helper
- 3,796
- 1,853
I fixed it.DrClaude said:Really?
DrClaude
Mentor
- 8,477
- 5,693
No, still wrong. But please let the OP answer now (this is the homework forum)..Scott said:I fixed it.
alijan kk
- 130
- 5
the B set isDrClaude said:No, still wrong. But please let the OP answer now (this is the homework forum).
(-0.5,0.5) f=b is the range
if the Ran f does not equal to B, then f is said to be into function , but this function is also one to one ,, so called injective ? thanks for the reply
DrClaude
Mentor
- 8,477
- 5,693
But is it one-to-one? Do you get a unique value for each ##x## in the domain of ##f##?alijan kk said:but this function is also one to one ,, so called injective ?
You should also check if it is surjective or not.
alijan kk
- 130
- 5
it is not ijective because, the range is not a subset ! "serjective but not injective" should be correct ? and serjective has range=B [-0.5,0.5]DrClaude said:But is it one-to-one? Do you get a unique value for each ##x## in the domain of ##f##?
You should also check if it is surjective or not.
Mark44
Mentor
- 38,039
- 10,522
What is "MCQS"?alijan kk said:MCQS is in the image
Mark44
Mentor
- 38,039
- 10,522
Noted...DrClaude said:But please let the OP answer now (this is the homework forum).
alijan kk
- 130
- 5
multiple choice questionMark44 said:Noted...
alijan kk
- 130
- 5
it is therefore requested kindly give me a hint or tell me the answerMark44 said:Noted...
Mark44
Mentor
- 38,039
- 10,522
Post #3 is a hint. A graph of this function would be helpful.alijan kk said:it is therefore requested kindly give me a hint or tell me the answer
By forum rules, we can steer you in the right direction, but we can't just tell you the answer.
alijan kk
- 130
- 5
domain is all real numbers,, and range is [-0.5,0.5]Mark44 said:Post #3 is a hint. A graph of this function would be helpful.
By forum rules, we can steer you in the right direction, but we can't just tell you the answer.
Mark44
Mentor
- 38,039
- 10,522
If you solve the equation ##y = \frac 1 {1 + x^2}## for x, do you get a single value of x for each y value? If so, the original function is invertible, and therefore one-to-one (i.e., injective).alijan kk said:domain is all real numbers,, and range is [-0.5,0.5]
If there is at least one x value for each number in the range, then the function is surjective.
SammyS
Staff Emeritus
Science Advisor
Homework Helper
- 11,987
- 1,579
Your thread would be improved if you were to display the image, rather than just showing the thumb-nail.alijan kk said:Homework Statement
MCQS is in the image,
Homework Equations
The Attempt at a Solution
as the range of this function is the subset of B , it is an injective function ?
option one is correct ?
Like this:
Attachments
Physics345
- 250
- 23
In your text there is a section for this clearly explaining how to find the proper range and domain and ******restrictions****** which is very important, I suggest you keep reviewing. Mastering your subject is key, that's when you really see the real benefits and understanding of Math.
mathwonk
Science Advisor
Homework Helper
2024 Award
- 11,934
- 2,195
an important tool for proving "surjectiveness" is the intermediate value theorem. do you have this available? it requires your function to be "continuous". on an interval domain. If so then it says that whenever you find two points of the target interval that are in the image of the function, then you can be sure that the whole interval between those two values is also in the image of the function. (In fact with a function like this one, there is really no other way to do this problem rigorously. I.e. even if you solve directly for the inverse images of potential values using root functions, you need that theorem to guarantee that the relevant roots actually exist. Of course you may be assuming that fact. I.e. do you know that square roots of non negative real numbers always exist? maybe they assume that in elementary courses.)
so either try a direct approach assuming roots exist, or try using that theorem, is my suggestion. in fact you might benefit from looking up that theorem just to expand your education, if it seems unknown. You might try as an exercise proving with that theorem that if f is a continuous function on R, and if points a,b,c exist with a<b<c, and with f(a) < f(b), and also f(c) < f(b), then f cannot be injective.i claim that if you use the intermediate value theorem, and look at the two values f(1) and f(-1), your problem is solved. it is up to you to see why.
so either try a direct approach assuming roots exist, or try using that theorem, is my suggestion. in fact you might benefit from looking up that theorem just to expand your education, if it seems unknown. You might try as an exercise proving with that theorem that if f is a continuous function on R, and if points a,b,c exist with a<b<c, and with f(a) < f(b), and also f(c) < f(b), then f cannot be injective.i claim that if you use the intermediate value theorem, and look at the two values f(1) and f(-1), your problem is solved. it is up to you to see why.
Last edited:
Similar threads
- Replies
- 23
- Views
- 3K
- Replies
- 11
- Views
- 3K
- Replies
- 3
- Views
- 1K
- Replies
- 12
- Views
- 2K
- Replies
- 15
- Views
- 2K
- Replies
- 3
- Views
- 2K
- Replies
- 7
- Views
- 2K
- Replies
- 4
- Views
- 2K
- Replies
- 1
- Views
- 2K
- Replies
- 20
- Views
- 2K
Hot Threads
-
Geometry: Similar Shapes
- Started by paulb203
- Replies: 116
- Precalculus Mathematics Homework Help
-
[ASK] Trigonometric Inequality
- Started by Monoxdifly
- Replies: 6
- Precalculus Mathematics Homework Help
-
What does this equation mean?
- Started by inuka00123
- Replies: 12
- Precalculus Mathematics Homework Help
-
Finding polar equation of a shifted cricle
- Started by farfromdaijoubu
- Replies: 6
- Precalculus Mathematics Homework Help
-
Intersection of a circle and a sine curve
- Started by vcsharp2003
- Replies: 26
- Precalculus Mathematics Homework Help
Recent Insights
-
Insights Why Entangled Photon-Polarization Qubits Violate Bell’s Inequality
- Started by Greg Bernhardt
- Replies: 26
- Quantum Interpretations and Foundations
-
Insights Quantum Entanglement is a Kinematic Fact, not a Dynamical Effect
- Started by Greg Bernhardt
- Replies: 11
- Quantum Physics
-
Insights What Exactly is Dirac’s Delta Function? - Insight
- Started by Greg Bernhardt
- Replies: 3
- General Math
-
Insights Relativator (Circular Slide-Rule): Simulated with Desmos - Insight
- Started by Greg Bernhardt
- Replies: 1
- Special and General Relativity
-
Insights Fixing Things Which Can Go Wrong With Complex Numbers
- Started by PAllen
- Replies: 7
- General Math
-
Insights Fermat's Last Theorem
- Started by fresh_42
- Replies: 105
- General Math