- #1
lbwet
- 8
- 2
Homework Statement
https://imgur.com/3H3pCkD
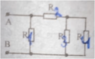
R is the resistance of each resistor, determine total resistance in the circuit. (see the image in the link above)
Homework Equations
R=1/R₁+1/R₂+1/R₃+... (in parralel circuit)
R=R₁+R₂+R₃... (in series circuit)
The Attempt at a Solution
I'm assuming that flow of electricity starts from point A. R₁ and R₂ should be considered parallel because charge can go in R₁ or R², thus resistance in those two resistors: 1/Rₜₒₜₐₗ=1/R₁+1/R₂ ==> Rₜₒₜₐₗ=R/2.
R₃ and R₄ also should be considered parallel for the same reason, thus in those two resistors Rₜₒₜₐₗ=R/2. Now, solving for resistance in the whole circuit I get: Rₜₒₜₐₗ=R/2+R/2=R, but that answer does not seem to be correct. Any help will be appreciated!
Attachments
Last edited: