Which is a Chord of a Hyperbola? AB or PQ?

[zorro]

Homework Statement

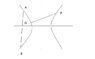
In the attached figure, which one is a chord of the hyperbola?
is it AB or PQ?

I am confused between both.
If AB passes through the focus perpendicular to the axis, it is called latus rectum which is a focal chord.
But in some figures I saw PQ as a chord.
Please explain me by defining chord of a hyperbola.

 

[tiny-tim]

Hi Abdul!

I don't think the term "focal chord" is in general use (wikipedia doesn't even mention chords in its hyperbola article).

I'd say that a focal chord is any line segment joining two points on the hyperbola,

but technically when the two points are on different branches, I'd say that it's the "infinite" line segment, that goes off to infinity in both directions, rather than the short one.

Think of the hyperbola as being a mirror … the reflection of any "short" focal chord would then be an "infinite" focal chord.

 

[zorro]

so a chord can be a 'line segment' joining any two points on the same branch of a hyperbola as well as on different branches ( in my figure both AB and PQ can be called as chords). Is it right?

 

[tiny-tim]

so a chord can be a 'line segment' joining any two points on the same branch of a hyperbola as well as on different branches ( in my figure both AB and PQ can be called as chords). Is it right?

That's my opinion , but I don't know whether there's general agreement on it.

 

[zorro]

Is there any book which has 'Chords of Hyperbola' topic in it?, so that we can arrive at a valid conclusion.

 

[tiny-tim]

I've no idea.

If you like, you can try a google book-search for "chord of a hyperbola" (do include the " and ") … that's by clicking "more" at the top of an ordinary google search.