Which path does this mechanism follow?

[marellasunny]

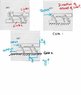
I found this mechanism(see image) in a very old book in the library.I was wondering if there is any mathematical technique(obviously geometrical) to find out the locus of travel that the links would take(case 1). Also, be able to calculate the displacements(case 2).

The problem with the given mechanism is that one of the links is a nonlinear curve, I would assume it as a quarter of circle with its entire length b.

Q.Also,would you know of any applications where such mechanisms are found?

 

[256bits]

Howdy
The two links you have labelled as "a" keep both surfaces parallel, as they rotate.
The link you labelled as "b" might be a spring or a latch mechanism - it is not obvious what the function is.

You might be able to find something similar to the simple mechanism in folding chairs, baby carriages although it will definitely not look the same as in the picture.

 

[marellasunny]

Howdy
The two links you have labelled as "a" keep both surfaces parallel, as they rotate.
The link you labelled as "b" might be a spring or a latch mechanism - it is not obvious what the function is.

You might be able to find something similar to the simple mechanism in folding chairs, baby carriages although it will definitely not look the same as in the picture.

If I take the case without the presence of the link b, then the mechanism would rotate on a locus with a turning radius 'a'. But, when the link b is included in the mechanism(as is shown in the figure), I'm sure the locus of movement would not be the turning radius 'a', the top link would move in a different path which brings me to my question- How do I find the path of movement of the link1(assuming link b is non-flexible)?

(Is it a superposition of the movements of the straight link a and the quarter circle shaped link b?)

IMO: This is a 1 dof mechanism with the link b making it a over-determinate mechanism.

 

[marellasunny]

A further attempt at the solution:
Assuming that the links 'a' follow a circular path of movement over a angle $\theta$, their new coordinates x2,y2 are given by:
x2
y2 = (rotational transformation matrix)*(initial coordinate matrix)
1

Not sure how to develop a transformation matrix for the curved link b up there though.

 

[siddharth23]

If the link 'b' is neglected, it would be a 4-bar mechanism with opposite links equal, the sort on mechanism used in railway engines. The link 'b' limits the circular motion of the two links named 'a' to upto a certain point. Like you said, the locus of a point on the links (3 which are moving) is probably an arc with radius 'a'.

Can't really think of a use for this mechanism off the top of my head. Maybe rocking chairs.

 

[marellasunny]

siddharth: In civil engineering, there is a terminology called 'statically indeterminate' structure i.e a structure where there are more links than needed. The use of the term 'statically' obviously indicated a 0 dof.

But, Is there an equivalent term in kinematics (to 'statically indeterminate')? I guess, the above mechanism should be probably expressed as 'over-determined' in case of kinematics, because there are more unknowns than equations.

Clearly, the above case is a over-determined system, right? We now have no option but to make link 'c' non-rigid i.e a spring. Do let me know of some theorems related.

 

[jehan60188]

i don't remember the name, i think kutzbach criteria
assume rigid links, and pin joints

DOF =3*(5-1)-2*6 = 0

it's not moving

 

[marellasunny]

i don't remember the name, i think kutzbach criteria
assume rigid links, and pin joints

DOF =3*(5-1)-2*6 = 0

it's not moving

Grübler's criterion.Yes,I calculated that i.e this would be a structure with 0 dof IF we consider the link c as a rigid link. But,in reality of today's mechanisms,link 'c' would have been a non-rigid spring. THEN, how would one go about calculating the kinematics of non-rigid links?

Take for example Ratchets, they have non-rigid links also. And for flexible belt pulleys, mechanical engineers have defined the term 'velocity ratio' to show the extension/contraction of the belts during op.

 

[Baluncore]

Q.Also,would you know of any applications where such mechanisms are found?

It is a parallel rule used by navigators to transfer a heading on their chart to the marked compass rose on the chart. It is walked across the chart by alternately holding one side down while moving the other. It is possible to traverse in any direction to anywhere on the chart. With practice it is fast and accurate.

This example seems to have a “piano wire” spring rather than the usual two knobs or buttons to hold it by. I don't know why it has the spring; maybe to read the protractor, as a handle, a spring to close it when not in use, or as a spring to take up the slack in the pins. Maybe the wire spring is a later users modification.

The graduated scale along the bottom of the upper rule is probably a protractor scale to read the angle of the linkage. But what is it read against? Maybe the piano wire spring is attached at the two fixed points and crosses the lower edge of the upper rule at the appropriate angle graduation. Since the spring attachment points are not parallel with the linkages the curvature of the wire spring will change as the linkage angle changes. That may be used here to linearise the protractor scale.

See; http://en.wikipedia.org/wiki/Parallel_rulers

 

[marellasunny]

The graduated scale along the bottom of the upper rule is probably a protractor scale to read the angle of the linkage. But what is it read against? Maybe the piano wire spring is attached at the two fixed points and crosses the lower edge of the upper rule at the appropriate angle graduation. Since the spring attachment points are not parallel with the linkages the curvature of the wire spring will change as the linkage angle changes. That may be used here to linearise the protractor scale.

See; http://en.wikipedia.org/wiki/Parallel_rulers

Wow!Great explanation on the scale. "Linearisation of a protractor scale"-it would be an amazing mathematical paper.

 

[Baluncore]

I found this mechanism(see image) in a very old book in the library.

I have been trying unsuccessfully to find a reference to the pictured parallel rules with the spring modification. I assume it was on page 367.
Please can you please let me know the Author, year and title of that book ?

 

[marellasunny]

I have been trying unsuccessfully to find a reference to the pictured parallel rules with the spring modification. I assume it was on page 367.
Please can you please let me know the Author, year and title of that book ?

Its a ebook in the cornell univ. database.This mechanism caught my eye because of its simplicity. I wanted to see if I could use kinematics to trace-out the exact path the mechanism would follow, but I don't quite know how!

http://ebooks.library.cornell.edu/c...dno=kmod005;view=image;seq=96;node=kmod005:46

 

[Baluncore]

Title: Five Hundred and Seven Mechanical Movements. Author: Brown, Henry T. Date: 1871.
This ebook is available free from Google Books as a pdf, (10.35 MByte).
The index to articles / figures shows: Rulers, Parallel. 322, 323, 324, 325, 349, 367.

367. A parallel ruler with which lines may be drawn at required distances apart without setting out. Lower edge of upper blade has a graduated ivory scale, on which the incidence of the outer edge of the brass arc indicates the width between blades.

Parallel rules were used in drafting to draw equally spaced cross hatched lines. That is the application of this particular modification. It seems to me that the fixed length brass arc, (with a variable chord and therefore variable radius), linearises the opening graduations on the ivory scale.

Other than that it is a simple parallel rule. The two diagonal flat brass links of traditional parallel rules are typically cut with that decorative profile. I cannot see what advantage there can be in the wasp-waist over the rule's gap when closed.

 

[wirenut]

If you download the e-book from the given link, on the next page, you will see a description of the item. Baluncore was spot on. The arc and scale are used to determine width between blades.

This is a fascinating read.
Thank you for the link.
Dan