- #1
degree451
- 1
- 0
I’m curious as to what the universe looks like according science theorists. So let’s say the “Big Bang” theory is correct. I have several models of what the universe could look like but I’d like to know which model is the most widely accepted one.
Model A:
Big Bang starts, universe expands, at some point the matter dump from the central point ends. In this model if we were far enough away the universe would resemble a lumpy sphere. All matter in the universe is contained within the relative outer shell of the sphere and the interior of the this sphere is void.
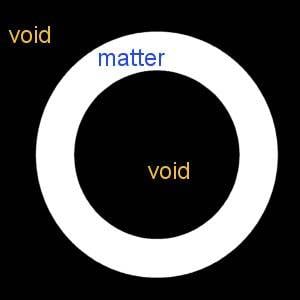
Model B:
Big Bang starts, universe expands, the central point continues to dump matter into the universe; it never stops. In this model again the universe is a lumpy sphere and the sphere is solid with matter filling all space from the outer shell all the way back to the center.
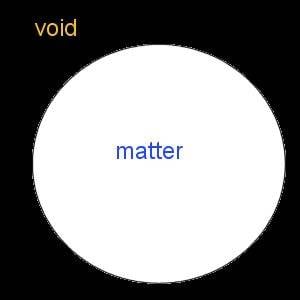
Model C:
Big Bang starts, universe expands, the central point stops dumping matter into the universe but after a period the central point begins dumping matter into the universe again and this cycle repeats N times. In this model the universe again is a lumpy sphere and each matter “spurt” creates spheres within spheres and the matter from each spurt is separated from the previous cycle’s by a spherical void. Of course if the expansion of one spurt is faster than the previous or slower than its successor then two spurts will eventually catch up with one another eventually banding together.

Model A:
Big Bang starts, universe expands, at some point the matter dump from the central point ends. In this model if we were far enough away the universe would resemble a lumpy sphere. All matter in the universe is contained within the relative outer shell of the sphere and the interior of the this sphere is void.
Model B:
Big Bang starts, universe expands, the central point continues to dump matter into the universe; it never stops. In this model again the universe is a lumpy sphere and the sphere is solid with matter filling all space from the outer shell all the way back to the center.
Model C:
Big Bang starts, universe expands, the central point stops dumping matter into the universe but after a period the central point begins dumping matter into the universe again and this cycle repeats N times. In this model the universe again is a lumpy sphere and each matter “spurt” creates spheres within spheres and the matter from each spurt is separated from the previous cycle’s by a spherical void. Of course if the expansion of one spurt is faster than the previous or slower than its successor then two spurts will eventually catch up with one another eventually banding together.