SUMMARY
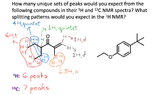
The discussion clarifies the confusion surrounding the splitting patterns and integrations of red and blue protons in a specific organic compound. The red protons exhibit a triplet splitting pattern with an integration of 6 H due to their chemical equivalence and the n + 1 rule, where n equals the 2 adjacent protons. Conversely, the blue protons show a quintet splitting pattern with an integration of 4 H, resulting from the contributions of adjacent carbons, where n equals 3 from one carbon and 1 from another, leading to a total of 5. This analysis is essential for understanding NMR spectroscopy in organic chemistry.
PREREQUISITES
- Understanding of NMR spectroscopy principles
- Familiarity with the n + 1 rule in splitting patterns
- Knowledge of chemical equivalence in protons
- Basic concepts of organic chemistry structures
NEXT STEPS
- Study the n + 1 rule in detail for NMR splitting patterns
- Explore chemical equivalence and its implications in NMR analysis
- Learn about the interpretation of NMR spectra for complex organic compounds
- Investigate the effects of adjacent protons on splitting patterns in NMR
USEFUL FOR
Organic chemists, students studying NMR spectroscopy, and anyone involved in interpreting splitting patterns in organic compounds will benefit from this discussion.