Why Can't I Use My Indicated Vector ds on a Gaussian Surface?

[logearav]

folks,
in my attached image, why can't i take the vector ds as indicated by me in pencil. i am confused. help will be greatly appreciated.

 

[jtbell]

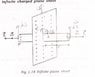
dS must always be perpendicular to the surface, and outward from a closed surface. Your arrows on the end caps are parallel to the end caps, not perpendicular.

 

[Cyosis]

It is often glossed over in calculations like these that you actually have to calculate the flux through every side of a Gaussian surface. There are three 'different' surfaces in this case. The two caps and the cylinder itself. The vector $d\vec{s}$ is always perpendicular to the surface. For the two caps this means you have to draw them as they are drawn in the picture. The directions are of course reversed.

For the cilinder the vector $d\vec{s}$ is the one you have drawn, the radial vector. This one is perpendicular to the surface of the cylinder at any point. The reason why this one usually doesn't get drawn or taken into account is that the electric field is perpendicular to ds in this case, which means $\vec{E} \cdot d\vec{s}=0$.

 

[pgardn]

What they said.

The electric field lines would all be horizontal pointing to the right on the right side of the sheet, and pointing left on the left side. So no E field lines would "penetrate" the curved part (cylinder) of your chosen Guassian surface, they would all run parallel to it.

 

[logearav]

Thanks a lot friends. I visited so many sites but could not get the answer. This proves that this site is full of brains. Thanks again...