Why Do Distant Objects Appear Dimmer Due to the Inverse Square Law?

[adjacent]

Homework Statement

This is not a homework problem but I'll post it here.It's just a question that came to my mind.

Why does distant objects appear dimmer?

The Attempt at a Solution

My answer would be the inverse square law.
For a point light,it can be quite easy to explain.As the distance increases,the amount of light falling per cm^3 decreases.
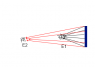
But what about a rod light(Whatever.See the diagram)?

I can argue that the amount of light falling on E2 is the same as the amount falling on the E1.What's wrong here?
Is this the way to think about this problem?Can you correct me?I know I am wrong somewhere.

 

[mafagafo]

I am no expert. Although we use mathematically an infinite number of light rays, this does not occur physically.
You have a finite number of photons, so dispersion still explains dimming.

 

[dauto]

Your picture doesn't say anything about the brightness of the object. It simply shows that the whole object can be seen from both points of view. The brightness is given by the inverse square law you mentioned.

 

[paisiello2]

My understanding is that a light source gives off a fixed number of photons every second (N/s). In your case with the rod it is still emitting a fixed number of photons per second but simply as a series of point sources (∑N/s).

If dimness is a measure of intensity of light at a distance which in turn is a measure of power per square meter then we can say that dimness is proportional to the flux of the number of photons (∑N/s/A) since each photon has energy associated with it.

Therefore, dimness for any type of light source would still follow the inverse square law with distance i.e. the number of photons arriving each second at a given point reduces the farther you move away.

 

[adjacent]

Thanks everyone.
Yeah.Assuming the rod as a series of points did the trick