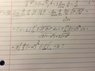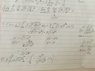Why Do My Answers Differ on These Limit Problems?

[Poznerrr]

Hey! Can somebody take a look on these two limit problems? I don't agree with the answer to #15, which is supposed to be 0 while I get infinity. #16 seems to ask to find the value of the sum...I posted a pic of my attempts to solve the problems below.

My attempts:

 

[pasmith]

#15 is asking for the limit *from above*. When \pi/2 < x < \pi, \tan x is negative.

However you are correct that the limit *from below* is e^{+\infty} = +\infty.

 

[Poznerrr]

#15 is asking for the limit *from above*. When \pi/2 < x < \pi, \tan x is negative.

However you are correct that the limit *from below* is e^{+\infty} = +\infty.

Ooooh, I see! Thanks!

 

[Fightfish]

For Problem 16, the approach should be to convert the summation into an integral thus:
\lim_{n \to \infty} \sum_{i = 1}^{n} \frac{3}{n} \sqrt{9 - \left(\frac{3i}{n}\right)^2} = \lim_{n \to \infty} \sum_{i = 1}^{n} \frac{3 \Delta i}{n} \sqrt{9 - \left(\frac{3i}{n}\right)^2}
where $\Delta i = 1$.
Then, it is straightforward to have a variable $\lambda = i / n$, so that in the limit $n \to \infty$, the summation becomes the integral
\int_{0}^{1}d\lambda\,\,3\sqrt{9 - 3\lambda^2 }

 

[Poznerrr]

For Problem 16, the approach should be to convert the summation into an integral thus:
\lim_{n \to \infty} \sum_{i = 1}^{n} \frac{3}{n} \sqrt{9 - \left(\frac{3i}{n}\right)^2} = \lim_{n \to \infty} \sum_{i = 1}^{n} \frac{3 \Delta i}{n} \sqrt{9 - \left(\frac{3i}{n}\right)^2}
where $\Delta i = 1$.
Then, it is straightforward to have a variable $\lambda = i / n$, so that in the limit $n \to \infty$, the summation becomes the integral
\int_{0}^{1}d\lambda\,\,3\sqrt{9 - 3\lambda^2 }

Thanks! I understand the substitution, but don't quite get how you came up with the limits of integration (0 and 1).

 

[Fightfish]

Thanks! I understand the substitution, but don't quite get how you came up with the limits of integration (0 and 1).

The variable $\lambda = i/n$ takes values between $0$ (i = 1) and $1$ (i = n), which are the corresponding limits of the original summation.

 

[Poznerrr]

The variable $\lambda = i/n$ takes values between $0$ (i = 1) and $1$ (i = n), which are the corresponding limits of the original summation.

The limits make sense then. I'm trying to compute the integral and something is really off...

 

[Poznerrr]

Here's what I get when I try to compute the integral

 

[Fightfish]

The integration is not correct; you need to use integration by parts - remember its an $u^2$ under the square root.

 

[Poznerrr]

The integration is not correct; you need to use integration by parts - remember its an $u^2$ under the square root.

I set u=sqrt(1-u^2) (du=-u/sqrt(1-u^2) and dv=du, so that v=u. But this didn't help much, since I still need in integrate sqrt. (1-u^2). It started to look more like inverse sine though.

 

[Fightfish]

Actually nevermind about the integration by parts; it's much faster to do a substitution directly on the original integral $\int d\lambda \,\,\sqrt{1-\lambda^2}$ - let $\lambda \equiv \sin \theta$ and proceed accordingly.

 

[Poznerrr]

Actually nevermind about the integration by parts; it's much faster to do a substitution directly on the original integral $\int d\lambda \,\,\sqrt{1-\lambda^2}$ - let $\lambda \equiv \sin \theta$ and proceed accordingly.

Yeah, I used trig sub and got the answer I was supposed to. Thanks for your help!