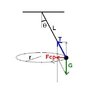
When a ball spins on a string, it rises due to the interplay of tension and gravity. The tension in the string has both horizontal and vertical components, with the vertical component counteracting gravity. As the ball spins faster, the tension increases, allowing the vertical component to exceed gravitational force, causing the ball to rise. The angle of the string with respect to the vertical also increases with speed, further contributing to the ball's height. Understanding this relationship clarifies how centripetal force and gravity interact in circular motion.