TheCanadian said:
I care about this integral as that is what is presented in the notes I attached above in equation (5.208). In the notes, they do not apply Laplace transforms until afterwards. This is why I think it is as simple as doing the math in a vacuum. Although I now see that in the notes that this integral is only valid for ##\Im \omega > 0##, otherwise there will be an additional complementary function present (i.e. a transient). And thus as you've been writing and mentioned in the literature, we must deform the contour to go below the pole if it is going down to 0 or negative in the imaginary axis.
I just spent a few minutes skimming the notes. They are appealing to causality arguments when evaluating the integral. This is a
physical argument, based on a reasonable expectation that a plasma is a causal system. They are
not looking at the integral purely mathematically in a vacuum, because the pure math way is ambiguous. So this is one way to get around the ambiguity without doing the initial value problem. There may be other ways, too, but in all cases the integrals will be considered in a context that makes sense physically.
TheCanadian said:
Returning to the first link I posted above, essentially my question boils down to what's stopping us from simply integrating (8.9)? At this point, before Laplace transforms are introduced, aren't ##\omega## and ##v## still complex-valued? In that case, sure, we know there is a pole at ##\omega = \vec {k} \cdot \vec {v}##, but aside from that particular point, our integration along the real line would go unimpeded unless ##\Im \omega = 0##. (I was just saying that one way to do this would be to apply Jordan's lemma and account for any poles via residue theorem, but I see now that the integrand considered does not satisfy the constraints on Jordan's lemma.)
Why would you expect ##v## to be complex valued from the get-go? It is a physical velocity, and the velocity integral is simply in Poisson's equation in the original differential-integral equation formulation.
Yes, you can try to tackle 8.9 directly. I don't know why you would, since even the notes themselves indicate that it is not properly defined. Landau was resolving that ambiguity with the initial value approach, and the notes use how 8.9 is not well defined to motivate why you want to try another approach.
TheCanadian said:
(I was just saying that one way to do this would be to apply Jordan's lemma and account for any poles via residue theorem, but I see now that the integrand considered does not satisfy the constraints on Jordan's lemma.)
Yep. Functions that look like ##e^{-u^2}## aren't very nice as the imaginary part of ##u## gets very large (either positive or negative).
TheCanadian said:
I am just failing to see why we have to treat this as an initial value problem and can't solve the above integral (8.9). If a Laplace transform is applied and we follow the prescription, all the steps make sense to me (thank you for that). But why must we treat this as an initial value problem and perform this transform in the first place? Is there no other way to get around it?
The causality argument used in the notes you attached are one such way to do it without doing the initial value problem. I had actually seen that approach many years ago while in school but had forgotten it. There may be other ways as well. But the "standard" way is to solve the initial value problem, and is the only way I remembered.
TheCanadian said:
Based on everything above, it seems the answer is because the equation (8.9) is itself incorrect as it assumed the perturbed distribution function has the form ##\exp (i \omega t)## despite there not being oscillatory behaviour for all time. I think that answers my question and clears up my confusion.
The problem is that there is physical information that is not being used so the equation is mathematically ill defined. It has nothing to do with the assumed dependence, which usually allows ##\omega## to be complex so is not necessarily oscillatory. Indeed, the Landau damping problem is solving for the imaginary parts of the frequencies of modes of the plasma.
TheCanadian said:
The main issue I was having with the first link was the sentence: "However, in doing so, we run up against a serious problem, because the integral has a singularity in velocity space, where
View attachment 220061 , and is, therefore, not properly defined." I just kept thinking that there were ways to go about solving the integral, but that solving that integral in (8.9) isn't what we actually want to find as it assumes a form of the solution that is incorrect.
Yes, the integral 8.9 is not what we want to solve. Not because of the assumed dependence, but because it is undefined for a regime we really care about. You need to find a way to make a physically meaningful definition: we now know two ways - the initial value problem and by using causality arguments. There may be other ways, too.
By the way, the same kinds of causality arguments can be used in other situations as well. For example, when solving the inhomogeneous undamped wave equation with Fourier transforms: you get poles on the real axis and correctly choosing how to dent the contour leads to a causal solution. Another way to get the correct solution is to add damping to the problem, set up the integral, then take the limit as damping goes to zero which forces you to dent the contour correctly around both poles. But in this case the causality argument is much easier to apply (at least for me) than in the Landau damping case.
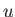 -axis, rather than above, because the integral is calculated by letting the pole approach the axis from the upper half-plane in
-axis, rather than above, because the integral is calculated by letting the pole approach the axis from the upper half-plane in
 -space."
-space."