formodular
- 34
- 18
Hi!
Where does the BRST transformation come from and why?
Peskin brings them into the Yang Mills Faddeev Popov gauge fixed action
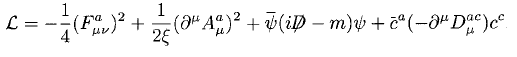
as a symmetry of the action after shifting ##A## (treating it as the outcome of a Gaussian integral over some field ##B##)
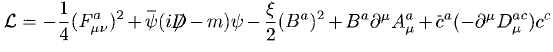
but the symmetry transformations are very complicated, mixing bosons and fermions (SUSY?):
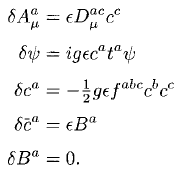
Why you want it and why it takes this form is mysterious.
This source tells you:
"Since we have more fields than gauge fields ##A##, to maintain the general idea of gauge covariance for physics, it is natural to look for a symmetry that encodes the definition of the gauge symmetry acting on ##A##, but also generalizes it in a consistent way on the new fields. This symmetry must interchange the gauge fields and the ghosts, in order to ensure the compensations between these fields in closed loops for any choice of gauge. Such a symmetry between fields of different statistics is the BRST symmetry."
Can this be expanded/explained more simply with more details (or even just explaining what it means fully), and can we say why we choose the transformations as written above, as it is very interesting!
Where does the BRST transformation come from and why?
Peskin brings them into the Yang Mills Faddeev Popov gauge fixed action
as a symmetry of the action after shifting ##A## (treating it as the outcome of a Gaussian integral over some field ##B##)
but the symmetry transformations are very complicated, mixing bosons and fermions (SUSY?):
Why you want it and why it takes this form is mysterious.
This source tells you:
"Since we have more fields than gauge fields ##A##, to maintain the general idea of gauge covariance for physics, it is natural to look for a symmetry that encodes the definition of the gauge symmetry acting on ##A##, but also generalizes it in a consistent way on the new fields. This symmetry must interchange the gauge fields and the ghosts, in order to ensure the compensations between these fields in closed loops for any choice of gauge. Such a symmetry between fields of different statistics is the BRST symmetry."
Can this be expanded/explained more simply with more details (or even just explaining what it means fully), and can we say why we choose the transformations as written above, as it is very interesting!
Last edited:
